Classes and objects

First up, here's roughly where we should be again. I've cut anything that was experimental, leaving the core of our code: backup what you've got, then copy this into your model.py file.

import random
import operator
import matplotlib.pyplot

def distance_between(agents_row_a, agents_row_b):
    return (((agents_row_a[0] - agents_row_b[0])**2) +
        ((agents_row_a[1] - agents_row_b[1])**2))**0.5

num_of_agents = 10
num_of_iterations = 100
agents = []

# Make the agents.
for i in range(num_of_agents):
    agents.append([random.randint(0,99),random.randint(0,99)])

# Move the agents.
for j in range(num_of_iterations):
    for i in range(num_of_agents):

        if random.random() < 0.5:
            agents[i][0] = (agents[i][0] + 1) % 100
        else:
            agents[i][0] = (agents[i][0] - 1) % 100

        if random.random() < 0.5:
            agents[i][1] = (agents[i][1] + 1) % 100
        else:
            agents[i][1] = (agents[i][1] - 1) % 100


matplotlib.pyplot.xlim(0, 99)
matplotlib.pyplot.ylim(0, 99)
for i in range(num_of_agents):
    matplotlib.pyplot.scatter(agents[i][1],agents[i][0])
matplotlib.pyplot.show()

for agents_row_a in agents:
    for agents_row_b in agents:
        distance = distance_between(agents_row_a, agents_row_b)

As an aside, note that the code:

    for i in range(num_of_agents):
        if random.random() < 0.5:
            agents[i][0] = (agents[i][0] + 1) % 100


and

for agents_row_a in agents:
    for agents_row_b in agents:
        distance = distance_between(agents_row_a, agents_row_b)

both pull out agents: the first using an index, the second the for-each loop iterator. There's good no reason for the difference, other than in the first case we were trying to understand the data structure. Now we understand it, we might want to change the former so it uses the for-loop iterator style; but in the best "if it ain't broke don't fix it" fashion, let's leave it as it is for the moment.

We're going to make ourselves a Agent class, in a new agentframework.py module, and put most of the code (bold, above) that initialises the agents in a random location, and moves them, into the agent class. Here's what our model.py will look like when we're done:

import random
import operator
import matplotlib.pyplot
import agentframework

def distance_between(agents_row_a, agents_row_b):
    return (((agents_row_a.x - agents_row_b.x)**2) +
    ((agents_row_a.y - agents_row_b.y)**2))**0.5

num_of_agents = 10
num_of_iterations = 100
agents = []

# Make the agents.
for i in range(num_of_agents):
    agents.append(agentframework.Agent())

# Move the agents.
for j in range(num_of_iterations):
    for i in range(num_of_agents):

        agents[i].move()

matplotlib.pyplot.xlim(0, 99)
matplotlib.pyplot.ylim(0, 99)
for i in range(num_of_agents):
    matplotlib.pyplot.scatter(agents[i].x,agents[i].y)
matplotlib.pyplot.show()

for agents_row_a in agents:
    for agents_row_b in agents:
        distance = distance_between(agents_row_a, agents_row_b)

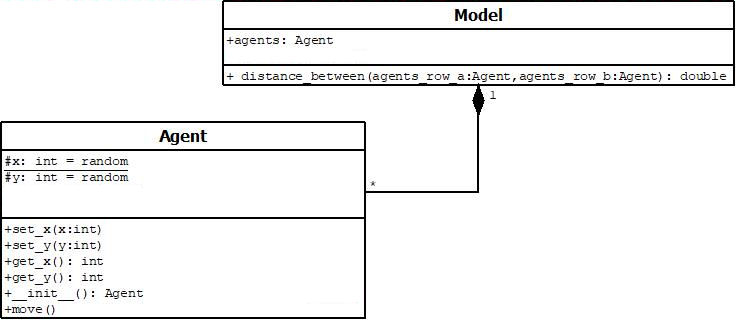
Here's the UML version. This is a class diagram. It says that there is one model with multiple agents it is responsible for the lifecycle of. The model will have a list of Agents, and a distance_between function. The Agents are going to have y and x coordinates. These will be protected to some degree and made available through appropriate accessor and mutator methods. They will also have a move method.

To start this process, make yourself a blank agentframework.py file in the same directory as your model.py. Open it up in Spyder, and define inside it an Agent class, with an __init__ method. Don't forget that all object methods have to have a parameter label to assign to the object when it is sent in; usually called self.

import agentframework at the top of model.py, and then convince yourself the two files are connected by somewhere in model.py making a single Agent:

a = agentframework.Agent()

Once you've got that running, we'll look at initalizing the Agent.