A semi-automatic method to build territorial partitions

Abstract

Introduction

    Our research problem emanated from the regional service of the french agricultural statistical institute (SCESS). They expressed the need to adjust and to use new territorial partitions more adequate to the providing of statistical information about " communal " agriculture. This paper occurs at the end of this work of research (1996-1999).

    So, our research situates at the interface of :
- a social demand for establishing pertinent spatial partitions and restoring a reliable statistical information (research program of INRA-DADP in Rhône-Alpes region, 1996-1999),
- a fundamental research about conception and evaluation of new methods of territorial cutting outs and areas aggregations (research program of PSIG, related to CASSINI research group, 1998-2000).

    In the first program, we expected to identify territorial pertinent entities to measure agricultural spatial leverage, by creating a spatial optimal partition with an appropriate method (Josselin et Laurent, 1999). This partition results from processing intercommunal agricultural flows and communes aggregation constrained by statistical confidentiality. We here introduce the complementarity of automatic methods of spatial classification and Exploratory Spatial Data Analysis.

    The objective of the second research program was to assess the use of genetical algorithms coupled to dynamical objects moving (called "drifted knowledge model" in the field of Distributed Artificial Intelligence, Chatonnay, 1997) to obtain pertinent spatial partitions. This new approach was to be compared with hierarchical clustering.

    This article presents a part of methodological results obtained in these two programs. We divided the process in different stages :
1 – define the problematic and find adequate statistical indices to measure partitions quality,
2 – test one of the common methods used by french statistics providers and users to build partitions from geographical flows : the hierarchical clustering,
3 – propose an alternate method to construct partitions avoiding hierarchical clustering defaults : genetical algorithms,
4 – evaluate, pour this new method, the contribution of the "drifted knowledge model" applied to genetical algorithms to the quality of the produced partitions,
5 – (in)validate and complement previous approaches by an exploratory data analysis,
6 – compare these steps, discuss their complementarity, and get some conclusions.
 

1. The question asked

1.1 Some flows in geographical space

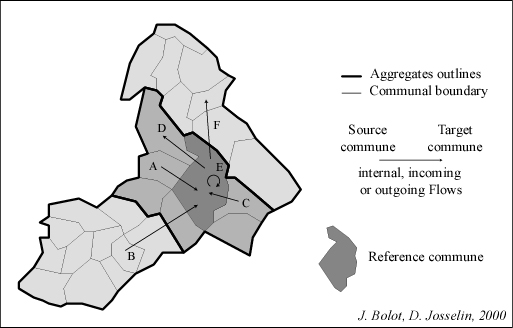
Fig. 1 – The concept of geographical intercommunal flow

    In this paper, we consider the example of agricultural intercommunal flows. Geographical objects taken into account for spatial aggregation are french communes (source commune and target one). They shape entities (aggregation or associations of basic entities) linked by flows, which represent farmed areas (fig. 1). If these flows occur in the entity, there are considered as internal : farmer uses the lands in his own commune (corresponding to his administrative location). If they link two different communes, they are external, more precisely outgoing for the source commune and incoming for the target one. In this last case, farming takes place out of the commune boundary. Per commune, the sum of internal and incoming flows is the available agricultural area.
 

1.2 Some territorial partitions to evaluate

    Several aspects of quality have been identified concerning quality of entities (or aggregates) (Bolot, Chatonnay et Josselin, 1999) :
- the territorial pertinence, indice computed with flows,
- the accuracy, which indicates the effect of entity size,
- the completeness, which makes relative the territorial pertinence evaluating the available information used for its calculation.

1.2.1 Territorial pertinence

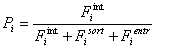
Fig. 2 - The territorial pertinence measure
with :   F_i ^int  the sum of internal flows within i
             F_i^out  the sum of outgoing flows within i
             F_i ^entr  the sum of incoming flows within i
 

1.2.2 Aggregates accuracy

1.2.3 Completeness of information

1.2.4 The quality measured at partition level

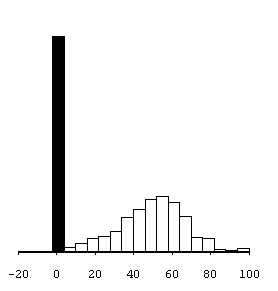
Fig. 3 – Statistical distribution of communal territorial pertinences in Isère
(in black : communes owning no flows)

    It is not the purpose of this article to detail the different aspects of partition quality. However, territorial pertinence will often be brought up later on, because it is used for partitions evaluation, even into aggregation methods.

1.3. Some territorial partitions to build

    There are lots of methods and algorithms which check for statistical association in a unique data board in order to classify objects. They are generally automatic (Celeux et al., 1989, Lebart, Morineau et Piron, 1995, Thiria et al., 1997). On our side, we propose four different, and sometimes complementary, adequate approaches to head aggregation process.

    The first one is a hierarchical classification, directed by constraints previously defined by expert (size of aggregates to be constituted, measure of aggregates quality, notably).

    The second one introduces a part of randomisation in the optimality quest, by using genetic algorithms.

    The third one add to genetic algorithms the use of a head method to direct the aggregation procedure. It is relative to distributed artificial intelligence (field of parallelism and optimal resources allocation into a network), especially the ""drifted knowledge model"".

    At last, Exploratory Spatial Data Analysis comes advantageously to complement these tree approaches, offering to informed users a graphic and interactive way to (in)validate automatic cutting outs and partitions and the possibility for "bad quality" aggregates to be recomposed.
 
 

2. Hierarchical Classification applied to the construction of territorial partitions

2.1.  Principle

    The principle is fairlay simple and based on the polarity concept. We aggregate successively communes which are "attracted" par some entities or existing "poles" (aggregates of communes). In our application, a pole P is attractive for a commune C when the part of the flow from C to P is important among whole internal and outgoing flows of C. The commune C is then « polarised » by P. It is then associated to P, the new set becoming a new pole, and the flows between C and P (in both directions) changing into internal flow in the new aggregate. We reiterate this process until obtaining a convenient partition for user.

2.2. algorithm

1 – On the whole map, we compute a matrix (n x n) associating couples of communes. For each couple A -> B, we calculate the rate R_A->B = flows from A to B / sum of outgoing and internal flow of A. R measures the part of flows from A to B among all flows concerning farmers having their administrative location in A (A->n).
2 – We identify the maximum value of R, and we aggregate A and B. These two communes constitute the first aggregate.
3 – We then process the new matrix ((n-1) x (n-1)), taking into account the status changes of  some flows of A with B. Indeed, as A and B compose a same aggregate, the number of concerned spatial entities reduced of 1 (or k with k more than 1) and all internal flows of communes A and B or outgoing from A to B or B to A become internal to the new aggregate. Outgoing flows of A and B to other communes outside the new aggregate (which may be A and B at the first step) keep their status (they are outgoing flows for this agregate), same for flows incoming from outside communes.
4 – We repeat the process until the complete aggregation of all communes and intermediate aggregates (except case with constraints of aggregates maximal size or process stopped by user).

The figure 4 shows an example of the algorithm, the figure 5 a resulting map, to which we can associate the distribution of territorial pertinences (fig. 6).
 
 

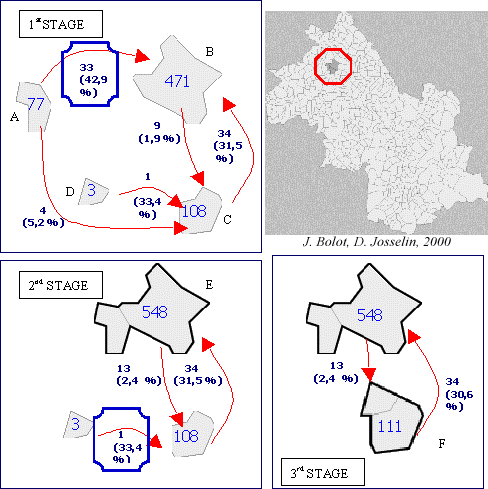
Fig. 4 – Communes aggregations by a hierarchical classification applied on flows
At step 1, we determine which entities are to be aggregated : communes A and B ; the 33 ha of agricultural flows of the commune A to the commune B correspond to about  43 % the whole of its own flows (value : 77 ha, including 33 h of flows A -> B, 4 ha for A -> C and 40 ha for internal flows of A). At step 2, the commune A is aggregated to the commune B. The aggregate E is made, owning (471 + 77 = ) 548 ha of internal and outgoing flows. This aggregate is however not enough strong (R = 31,5 % of C -> E) to attract the commune C
(R = 33,4 % of D -> C). At step 3, the aggregate F is created, by aggregation of C and D.

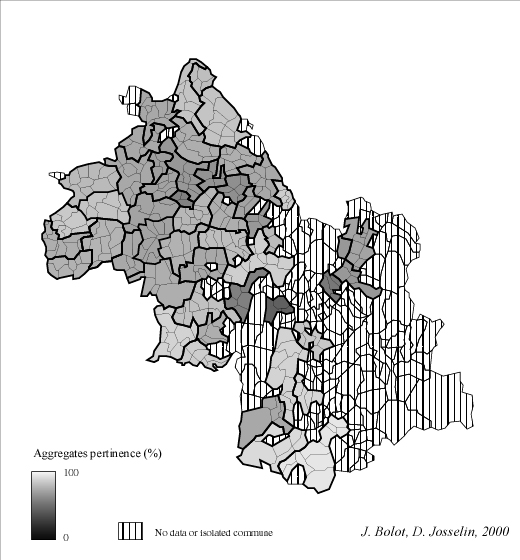
Fig. 5 – Aggregates of communes (between 3 and 10 communes per aggregate)  made with hierarchical classification

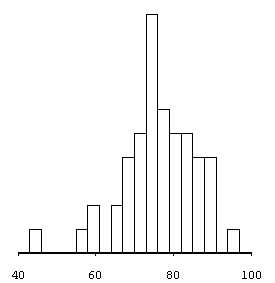
Fig. 6 – Statistical distribution of territorial pertinences of aggregates (cf. Fig. 5)
(mean = 77 ; median = 77 ; 50 aggregates)

2.3. discussion

    The results are good, if we refer to the territorial pertinences distribution (fig. 6), because it is based on polarity :
- either, hierarchical classification englobes only a part of individuals, those for which it was "easier" to aggregate,
- or, close to the process end, there appear some highly attractive poles, including lots of communes and providing good scores of pertinence.

    This method also has the advantage to enhance the poles attracting flows and to be reproducible, running onto an univocal solution at any step. It has been validated by statistical spatial data providers (INSEE, in France, notably). Formed aggregates are quite looking to each others, considering their shape and their size.

    The major disadvantage of this method is that, each step depends on the previous one. An error, an uncertainty, or a particular configuration of flows at a given step of aggregation procedure, may generate a bad orientation of the process, orientation whose all subsequent stages might suffer. It thus can load to an impoverishing of the information essential for a good analysis of flows and to the risk a not dominated error in hierarchy to be propagated. In fact, communes and entities in relation do not have a clear and permanent view of reciprocal links (through flows computation) in the studied space. Each level in hierarchy has an only local knowledge of these relations, depending on the previous processed aggregations.

    Moreover, to aggregate the whole set of communes, we must wait for the last step of processing. At any time of the process, the less polarised communes are set aside, making appear an interstitial space delicate to be analysed or cut out.

    So do we propose other methods which may be able to handle that problems.
 

Fig 7 - Screen of the software ASD (Directed Spatial Aggregation) for hierarchical classification (J. Bolot)
 

3.  Genetic algorithms applied to the construction of territorial partitions

3.1. Principles

    At the beginning, genetic algorithms must dispose of a first population. Indeed, they do not create life, they just modify it. This means the first individuals do not have to be very efficient, since the process looks for improving the populaion characteristics. Their initial performance only influences the convergence speed of the algorithm.

3.1.1. Individuals selection

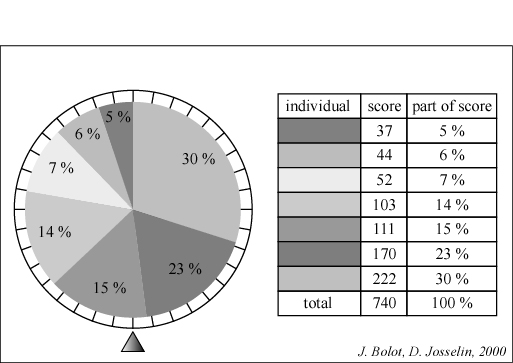
Figure 8 - Individuals scores and the "fortune wheel"
For example, the 6th individual has a note of 170. This value represents 23 % of the total of notes (740).
Its probability to be chosen at the time of selection is thus 23 %

    The precept of selection is quite simple (fig. 8) :
- one measures the « quality » of an individual, its « score »,
- according to this score, one calculates for this individual the part of score corresponding to its selection probability (value of note / sum of attributed notes). This probability is greater when the individual is considered as good for the evaluation function.

    This random selection under constraints of probability permits to keep "good" individuals. Moreover, potentially, all possibilities can be explored.

3.1.2 Individuals reproduction and mutation

    The crossing consists of cutting two individuals by a identical manner and assign to one the characteristics of the other and contrariwise. The cut position is chosen randomly.

    The mutation purpose is to modify randomly the characteristics of an individual. In fact, the mutation intervenes occasionally. It permits to broaden a little the solutions exploration domain.
 

3.2. Application to spatial aggregation and territorial cutting outs

3.2.1. Creation of an initial population of partitions

    To generate a set of initial partitions, we use what we call "gluttonous algorithm" (!). They choose a commune for starting, then construct aggregates by iterations, defining their outlines according to contiguity degree and maximal size of aggregates which are previously fixed.

    According to this principle, this algorithm can create as many partitions as there exist entities,  even more, if we exceed the first degree of contiguity. Moreover, this method can randomly, for each process of aggregate creation, define a contiguity level. In every cases, these partitions are not optimised. They constitute the initial population.

3.2.2. Reproduction principle applied to territorial partitions

1 – We first apply a break in the partition and delimit two distinct areas. Starting randomly from a  commune, we generate a first area by grouping some bordered communes. This procedure which define a first area, can be stpped at any time, by a random function. The second area is the complementary set. This ensures the continuity of the cutting. The size of the two area is, in most of cases, different.

2 – Along this cut, we apply the previous principles to modify or to add aggregates. Potentially (it is expected), the break can disturb the spatial partition. Some aggregates may be split in two parts and some communes may stay alone. The reproduction process permits, by swapping isolated or aggregated communes :
- to modify existing aggregates by associating to them isolated communes,
- to create new aggregates,
- sometimes, not to change anything.
 
 

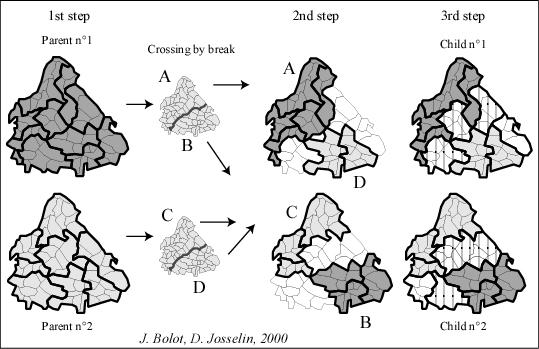
Figure 9 : Application of reproduction principle to spatial entities
A break into the two parent partitions (first stage) triggers an exchange of two groups of aggregates (A,B) and (C,D) between the partitions (becoming thus (A,D) et (C,B)). Interstitial space next to the break (in white at second stage) is then rebuilt by aggregation (third stage).

3.2.3. The selection of pertinent partitions

    This selection function has the advantage to compensate the aggregates accuracy by their number : more important is the number of aggregates, more little they are, more their quality may be low, but their greater number favors a high value of the sum of their pertinence.

    Optimisation is realised according to the calculated score. The score of each partition (sum of aggregates territorial pertinences) is set by dividing the note by the sum of the whole notes of the partitions population. Each score determines the probability for lottery drawing (« fortune wheel »).

3.3. Discussion

    Indeed, they consume a lot of time for processing. While the hierarchical classification follows the same iterative process, genetic algorithms, because of introducing a part of randomisation, may doubtless produce different partitions at any process execution. Let's add the learning procedure must be stopped by user.

    Moreover, genetic algorithms consider the whole set of communes in the studied space, while hierarchical classification includes more and more communes during the aggregation procedure. This maybe explains in general the "bad" scores of aggregates pertinence of genetic algorithms (fig. 11) compared to hierarchical classifications, these last ones taking into account firstly the "good" aggregates.

    In fact, genetic algorithms look for obtaining a high sum of scores. This may inquire about the relation between the aggregates accuracy by their number, which is not really proportional reverse, and would earn to be deepened. Moreover, the break process (reproduction) tends to make evolve the partition to be composed mainly of little aggregates (fig. 10). These aggregates can be numerous, and the sum of their quality, maybe high, can correspond to low values of mean and median. They also are very different, by their shape and their size.

    Another important characteristic, proper to genetic algorithms, is that they support the idea there doesn't exist a unique optimal solution, but a set of possible ones, among whose there are acceptable ones. Moreover, they explore all possibilities and are capable of altering what is granted at any time of the process, contrariwise to methods such as hierarchical classification.
 
 

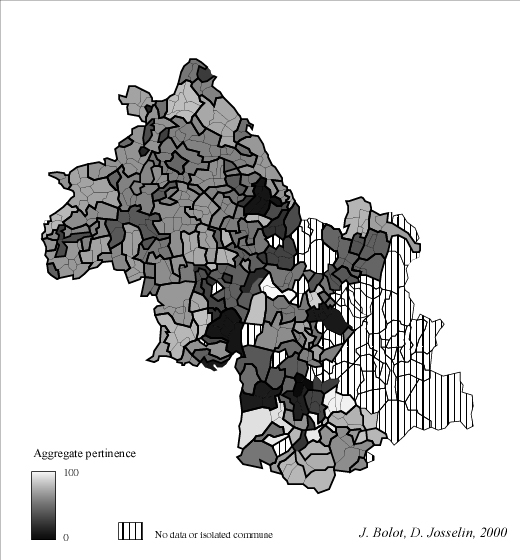
Fig. 10 – Some aggregates of various sizes constructed by genetic algorithms

 

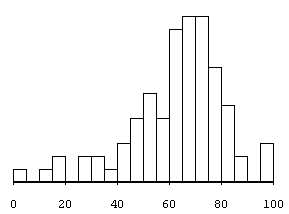
Fig. 11 - Statistical distribution of various aggregates pertinences (see fig. 10) made by genetic algorithms (mean = 62 ; median = 63 ; 87 aggregates)

4. Genetic algorithms assisted by the "drifted knowledge model"

4.1. The directed mutation

    So, directed mutation is the result of a random process and several modifications due to the analysis of the candidate genome. The objective of this analysis is to create a similar individual, disposing of de characteristics considered as relevant.

    In practice, we have to orient genetic algorithm according to a criterion which evaluate the activity of the aggregate of communes in « time» (this is a sorted sequence of events). This activity memorised while genetic algorithm convergence, will permit to choose, among candidate partitions, the most pertinent. To reach that goal, we use the "drifted knowledge model".

4.2. The "drifted knowledge model"

    Mathematically, each link between nodes of the graph is incrementally computed according to time with a quite simple function (fig. 12).
 
 

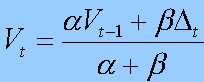
Fig. 12 - The "drifted knowledge model"
with :    V the value at t
             Delta the activity evaluation on the last period of time
             Alpha and Beta represent the relative importances of        present and past (Alpha + Beta = 1)

    V and Delta are expressed in the same metric. If Delta is greater than V modulo the rate Alpha / Beta, then the link becomes stronger, otherwise it is weaker.

    For territory cutting out, we didn't have enough temporal information about flows evolution to process it directly. Nevertheless, because of genetic algorithm use, we have an ordered classification of individuals according to their territorial pertinence during process. This ordered relation can be used instead of time. Thus, we construct incrementally the links between neighbouring communes from proposed partitions. Starting by the "worst" ones and finishing by the "best" ones, we can built, at each iteration, a graph which describes links between communes. This graph can be used to deduce, for a given commune, the interest to belong to any aggregate. Moving a commune from an aggregate to another is then considered as a kind of mutation.

4.3. Algorithm

ii – Application of the "drifted knowledge model" under constraints of contiguity between communes
Partitions i are sorted by their territorial pertinence
Calculation of the Link between two adjacent communes A and B : L_AB
Initialisation of all L_AB to value : 0
For all partitions i
  For all  communes A of i
    For all communes B contiguous to A
      If A and B belong to the same aggregate of the partition i then DELTA = 1
      Otherwise DELTA = 0
      Calculation of  L_AB(i) = (Alpha * L_AB(i-1) + Beta * DELTA) / (Alpha + Beta).
    End
  End
End

iii – Using the link L_AB to head mutations and crossings
We know, for each couple of contiguous communes A and B, the link L_AB, taking into account the criterion of appurtenance to the actual aggregate (Beta * DELTA) or to past ones (because Alpha * L_AB includes the past Beta * DELTA). By adjusting Alpha and Beta (with Alpha + Beta = 1), we counterbalance the past and the present to orient the mutation choice, according the known L_AB. At the time of genetic algorithm process, some mutations or crossings are proposed. Some of them are selected, according to the "drifted knowledge model", notably when the L_AB values are high. In other cases, the "model of drifted knowledge" won't intervene. The procedure of mutation directed by this metamodel tends to strengthen the existing optimal partitions.

4.4. Discussion

Moreover, two main problems appear :
- The disparity of aggregates in terms of shape and size is greater, this fact having a direct influence on the pertinences distribution shape,
- The objective to associate isolated communes to aggregates created by "drifted knowledge model" is not reached ; a possible explanation may be the necessary learning duration which has been too short ; other reasons have to be found.
 
 
 

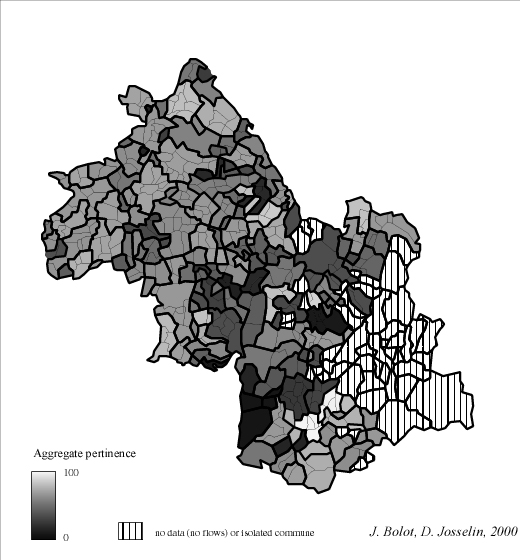
Fig. 13 – Somme various aggregates of communes constructed by genetic algorithms directed by the "drifted knowledge model" (alpha = 0.3 and beta 0.7)
 

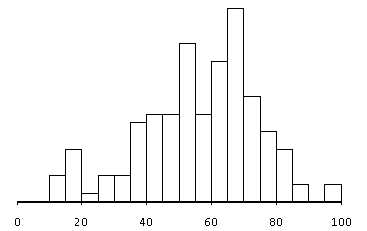
Fig. 14 - Statistical distribution of aggregates territorial pertinences (see fig. 11)
(mean =  56,7 ; median =  60 ;  140 aggregates)

 

Fig. 15 - Screen of the software ASD (Directed Spatial Aggregation) for genetic algorithms (J. Bolot)
 

5. Exploratory Spatial Data Analysis

5.1. A semi-automatic method

Fig. 16 - Agricultural external flows complexity (example in the Franche-Comté region, in France)

    Another reason comes directly from quality measurement. Indeed, numerical indicators at partition level feel to us too reducer. It may be opportune, in the quest of the optimal partition, to give back to user the possibility to evaluate quality :
- Globally, by studying spatial and statistical distributions of aggregates territorial pertinences,
- Locally, by precisely identifying the individual(s) (communes, flows, or aggregates) which own weak pertinence.

    Finally, we noticed the great amplitude of aggregates pertinences in statistical distributions when they were issued from genetic algorithms. In front of this result, user must be able to modify the partition as he wishes and handle "bad quality" aggregates. If some aggregates do not convene, it may be interesting :
- to exchange two communes between two aggregates,
- to associate a set of communes to an existing aggregate,
- to create a new aggregate.

    These modifications engender changes in flows status (some outgoing flows may become internal to a new aggregate) suited to be dynamically easy detected. User can also make playing his own and subjective knowledge about local environment (practical experience, planning purposes, social or political coercion, etc.).

5.2. The ARPEGE’ software : a tool to Analyse Robustly in Practice and Explore Geographical Environment

    Exploratory Spatial Data Analysis (Fotheringham, Brunsdon, Charlton, 2000) belongs to the field of Exploratory Data Analysis (Tukey, 1977, Haoglin, Mosteller, Tukey, 1983) ; within ARPEGE' software, it is allowed because of :
- dynamic linking between different objects classes such as communes, flows and aggregates, that are all associated to an adequate geometry and back map,
- statistical representations (here essentially distributions) describing individuals of each objects class,
- the possibility to select on screen particular objects (communes, flows or aggregates), depending on either their statistical characteristics (weak values of pertinence, for example), or their spatial repartition (graphic choice on the map),
- the permanent update, by triggers, of aggregates pertinences distributions, permitting to evaluate the impact of the proposed modification on the partition quality.
- User can (in)validate his hypothesis onto crossed sub-populations (and sub-populations issued from these sub-populations, etc.) from initial populations of objects (communes, aggregates and flows),
- The whole set of objects is managed by a high level object, called "visioner" (fig. 17), which plays an equivalent role as a CASE tool, and permits to know at any time, the structure of the data base (by identifying the statistical graphics, the elementary objects classes et the different spatial, structural or functional relations).

    Association, aggregation or inheritance relations are notably supported (generalised by n to m model), by a management by lists and by the objet orientation of the programming language. The binary, ternary or n-ary relations have to be implemented as objets, with all their pointers.
 
 

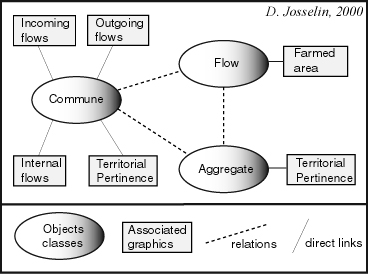
Fig. 17 – The « Visioner » : a kind of CASE tool to manage objects, statistical associated graphics and relations ;
one can retrieve the studied application with its flows, communes, aggregates, their relations and their statistical representations

 

Fig. 18 – ARPEGE' software (D. Josselin) : exploratory analysis of relations between communes, intercommunal agricultural flows and territorial partition (here : an administrative territorial partition zoning agricultural areas)

    In figure 18, user selected, in an histogram, all communes having weak incoming flows (in terms of farmed surfaces). He can analyse their spatial repartitions and distributions in graphics of others variables concerning communes. He then notices that these communes also own, for most of them, weak internal and outgoing flows. He can visualise the involved external (i.e. incoming and outgoing) flows and the agricultural regional areas they belong to. He knows finally the territorial pertinences of concerned communes and aggregates. In this example, aggregates are "little agricultural regions".
 

Fig. 19 – Modification of aggregates in a partition by an exploratory spatial data analysis in ARPEGE’ software (D. Josselin)

    As we previously saw, ARPEGE' software also offers to user some functionalities to modify territorial partitions (fig. 19), such as zooming, areas or lines drawing, exchanging communes between aggregates, moving a set of communes from an aggregate to another, creating new aggregate by grouping aggregates or communes. These functionalities are dedicated to aggregation procedures and flows analysis.

5.3. Discussion

    Behind an apparent ease, it appears that taking into account, simultaneously, three types of objects in relation is not an effortless way. Indeed, it is necessary to integrate different scales during same analysis process, while associating statistical reliance between objects of same or distinct classes. Moreover, the possibility of having samples or sub-populations instead of the whole population may be delicate to manage especially when this process occurs during the same time. In a more general view, we may say that "exploratory" is closely linked to "combinational".

    But modifying existing partitions is rather useful, especially because of potential impact dynamic evaluation. It offers to user to keep permanently in touch with individuals et to dominate, in this stage, the aggregation process, according to a reliable analysis of the distribution of aggregates territorial pertinences.
 

Conclusion

    We shall not  make a definite choice among these methods, this choice depending strongly of the domain and the view the user has on this problem. This user may be statistician, data manager or provider researcher, etc.

    We also presented that the different methods we used have, for each of them, their own qualities and defaults. In this paper, we showed the complementarity of these methods, using them one after the other. We expect better results by introducing directly in the aggregation process some exploratory function, which might, for example, head mutations. In other terms, their concomitant use might give better results than applying one of them or both separately. But, at this step of our work, we ensure our proposal of coupling automatic and exploratory methods is useful and has to be develop in a close future.

    Nevertheless, we can compare them using several criteria of quality (on a broad sens), depending on  :
- The produced partition (pertinence, completeness and aggregates accuracy, corresponding between pertinences distribution and awaited results by experts),
- The aggregation method which was employed (fastness, convergence and resistance to noise),
- The user look (use ease, fit-to-use, domination of partitions construction process) ; let's notice the profile of user in figure 20 corresponds approximately to our applicants : "a wary statistician, careful to use tested, fast and dominated  methods ».

    A vertical reading of figure 19 permits to separate two types of approaches :
- The first one corresponds to a statistical approach of producing territorial partitions ("the user" of fig. 20) ; his preference clearly goes to methods such as hierarchical classifications, eventually associated to (upstream and) downstream, exploratory analysis,
- The second one convenes more to researcher, whose purpose is the quest of optimality and a permanent discussing of what is acquired, by introducing a part of randomisation in procedures and algorithms ; in this case, exploring takes all its sens and an association genetic algorithms / exploratory spatial analysis may be convenient :
    * exploration of all possible solutions by genetic algorithms
    * upstream and downstream exploration of geographical data with Exploratory Spatial Data Analysis.
 
 

APPROACH  POINT of VIEW	Hierarchical Classifications	Genetic algorithms	Genetic algorithms +      "model of drifted knowledge"	Genetic algorithms + ESDA
PARTITION, AGGREGATES    - pertinence    - completeness    - accuracy    - pertinences distribution shape	++  -  0  --	+  -  ++  0	++  -  ++  0	+++  -  +++  ++
AGGREGATION METHOD    - fastness    - convergence    - resistance to noise	+++  +++  -	-  +  ++	--  +  ++	---  ---  +++
USER    - ease    - fit-to-use    - process domination	++  ++  --	++  0  --	+  -  +	-  +  ++

Fig. 20 – Evaluation of the quality under several aspects according to the different methodological tested approaches (from --- very bad to +++ very good)
 

    Besides, an horizontal reading of this same table (fig. 20) shows several elements about quality that may orient further investigations :
- information completeness might be integrated in partition creation process,
- a quantitative indicator associating territorial pertinence and aggregates accuracy remains to be established,
- objective descriptors of pertinences distributions shape might be helpful to user in his approach,
- an optimal balance (depending on the goal) between randomisation and the crossings and mutations direction is to be defined and argued,
- defining user specifications is very important, because it helps developers to adapt the software (do we propose an open system, a friendly interface, or both ?); these aspects are delicate to manage in such projects because they relate the duality of research and action.
 

References