Storing Voronoi diagrams in geographical databases

Jean-François Hangouët
Laboratoire Cogit
Institut Géographique National
2-4 avenue Pasteur
94165 Saint-Mandé Cedex
France
E-mail: Jean-Francois.Hangouet@ign.fr

Abstract

Two-dimensional cartographic wholes are stored in the computer as mono-dimensional lists of so-called geographical objects. Although disposition of objects is as desirable as individual presence for cartographic representation (generalization) and geographical analysis, configurations are only implicitly stored, by means of coordinates. While the full reconstitution can be said to be left to the eye and appreciation of the human operator upon displaying, any automated handling of geographical data involves automated reconstruction of some kind.

Reconstruction is often performed with purpose-oriented tools, the more obvious and the more famous of which may well be the Delaunay triangulation, clearly dedicated to the elicitation of proximity relationships. Either as such, or in the dual form of the Voronoi diagram on points, we consider it however to be a purpose-oriented tool indeed inasmuch as before triangulation can be computed, specific points from the data must be chosen, the constraint being that they be representative enough for the wished-for application.

A similar yet bias-free structure exists: Voronoi diagrams on segments, brought into geomatics by Christopher Gold. These diagrams also cast separate cartography-worthy objects into a planimetric whole, by allocating portions of the plane with closest points to every atomic part from the features (every segment, every junction). But now, involving everything from the available geometry of the features, they account fully of them, and can be said to be data-induced structures. Such diagrams can thus be pre-computed, and it is the aim of this paper to describe in what form they can be stored to meet efficiently quite remarkable a range of basic spatial queries.

The paper deals not actually with how to compute Voronoi diagrams on segments (referring to literature from the field of computational geometry), but with how, once computed, they can be stored in relation to the available spatial data. One "intrinsic" diagram per object, and combination methods for "combined diagrams" when several objects are retrieved together, are advocated. Edges of a Voronoi diagram are geographically classified as "internal edges" (within the contour of an object), "external edges" (left or right from an object, separating components of its own trace), "interface edges" (separating components from two different objects). Edges are also geometrically classified (segments of lines equidistant between point and point, of lines equidistant between segment and segment, of parabolas equidistant between point and segment). Useful attributes for edges are described (end points, minimal-maximal distances to objects etc.) as well as basic calculation methods (length of an edge, where to find on it a point at a given distance from the object etc.).

In addition, a variety of basic but recurring and often fastidious spatial queries are shown to be made simple not only by using Voronoi diagrams, but by using them with the advocated structuration. Convex hull, Minimum Spanning Tree, dilation, erosion, opening, closure, skeleton, Hausdorff distance between lines, Hausdorff distance between areas, the Bouligand-Minkowski fractal dimension, and water-lining (as re-introduced recently by Albert Christensen, yet from another point of view) are described shortly.

Keywords

Voronoi diagrams, geographical databases, cartometry, automated spatial analysis, computational geometry

1. Introduction

The paper is meant to describe how Voronoi diagrams can be integrated in vector geographical databases and GISs. In this introduction, a few preliminary considerations are made, separately (first on vector GISs then on Voronoi diagrams), not to expose detailed theories of either, but to contextualize the present work in broad terms and with general references from the two perspectives.

1.1. Vector geographical databases

In this section, vector geographical databases are presented with an emphasis on the representation of geometry.

1.1.1. Generic description

In geographical databases, geographic features are represented by means of objects of various geographical types. What distinguishes vector from raster databases is the way the inscription of the object on the ground is stored: by means of pools of pixels in raster databases, by means of successions of coordinates in vector databases. The paper addresses vector databases.

1.1.2. The geometry of objects

Accordingly, what is meant by "geometry" of an object in the following is the list of the successive points used to denote its inscription on the ground. We consider it to be equivalent to the list of the successive segments, those joining the successive points. This consideration however needs justification, as general conceptual models for "geometry" usually make room for interpolations of other kinds [see e.g. the definition of GM_CurveSegment, (OpenGIS 1999: 20): the list of points is equipped with the indication of their interpolation]. Our restriction is motivated by at least three observations:

Geographic data are captured point-after-point, not curve-by-curve.
Basic geographic data in vector GISs are stored as lists of points, not as curve functions.
The traditional way of denoting geographic limits (coasts, borders...) and geographic traces (roads, rivers...) is to indicate meaningful posts, between which interpolation is made by straight lines. This for example is how routes are usually described, this is also how Strabo advocates how the limits of the world should be apprehended: it will suffice to fill out and complete the outline of (the inhabited land) by joining with a straight line the extreme points reached on the coasting-voyages made on both sides of the inhabited world...(Strabo 2.5.5)

The underlying "explanation" behind each of the three reasons is, of course, that straight lines are easier to deal with than strangely-shaped curves (which is true for computer-assisted capture and computer storage, and for the general apprehension of geographic phenomena as well).

1.1.3. Location vs. configuration

This geometry of traces and contours provides no indication beside location: shapes of objects, dispositions of groups of objects, mutual distances between objects are contained in a latent state only. These are usually elicited by application-specific methods (e.g. selection in a specific box or a perimeter, or Delaunay or Voronoi structures on specifically-chosen points, or segmentation algorithms with specific thresholds etc.), before the application itself (e.g. generalization, or expert object analyis, or integration of exogeneous data etc.) may be said to start.
The Voronoi diagram on the full of the available geometry (i.e. on points and segments), as described section 2 of the paper, is a way to (re)constitute the configuration of objects independently from any application, yet with benefit for many applications since recurring difficult operations are made easier with it, as illustrated in section 3.

1.2. Voronoi diagrams

Voronoi diagrams turn out to be useful structures to model the natural cimentation in their global space of objects given seperately.

1.2.1. General definition

Objects of a same space (not a polygon and a differential equation) are given separately.
The given group of objects is called the figure in the following.
Each separate object is called a site in the following.
The Voronoi diagram of the figure is the attribution, to each object, of all the points in the space that are closest to it than to any other object, according to some distance.
Cells are thus constituted. Cells are limited by boundaries equidistant with other sites.

1.2.2. Varieties

Voronoi diagrams, according to this general definition, may be defined in spaces of any dimension (2, 3, n...), with any kind of distance (not necessarily the euclidean distance), on any kind of separated objects (points, and/or segments, and/or curves...), with any kind of distance minimality (minimal, second-minimal, nth minimal etc.). (Okabe et al. 1992) describe many varieties.

1.2.3. Computation

The computational time complexity of Voronoi diagrams is O ( n . log n ), when the figure is composed of n sites. Several optimal or practical strategies have been designed (divide-and-conquer, incremental, sweepline etc.). It is not the purpose of this paper to describe construction algorithms, as extensive documentation can be found in (Okabe et al. 1992), (O'Rourke 1995), (Boissonnat & Yvinec 1995), and from Computational Geometry Resources, Prisme project, and of course Christopher Gold's Voronoi Web Site. Martin Held has produced a recent publication on the subject, an extended abstract of which can be found here.

1.2.4. Applications

Christopher Gold's Voronoi Web Site shows that Voronoi diagrams are everywhere, from the eggs in the frying pan to the galaxies in the Universe, and provides extensive lists of applications of Voronoi diagrams in many fields of science and of technology.

1.2.5. Voronoi diagrams in this paper

The Voronoi diagrams here described for vector GISs are those introduced into geomatics by Christopher Gold during the last twenty years (see the collection of his Voronoi-related papers here), and have the following characteristics:

Sites are points and segments,
Space is the euclidean plane.

Cells are limited by edges that are segments of straight lines (of bisector lines when equidistance is two segment sites, of mediatrix lines when equidistance is between two point sites) and segments of parabolas (when equidistance is between a segment site and a point site).
In this paper, both by convention and for practical reasons, the endpoint of segment is considered to make a separate site, and the line orthogonal to the segment at the endpoint is considered to be the Voronoi edge between the two sites. This, in all, thus makes 4 kinds of edges (see figure 1 below).

"Four
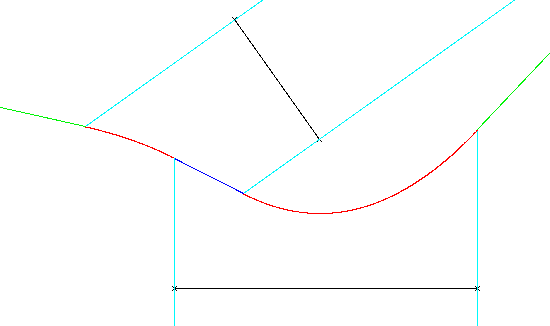
Figure 1: The four kinds of Voronoi edges
parabola (red), mediatrix (green), bisector (deep blue), degenerate (light blue)

Edges meet at nodes.

Note: all segments and points composing the geographical objects' geometries - i.e. all the available geometrical information - are taken into account by the diagram.

2. Storing Voronoi diagrams

This section describes how Voronoi diagrams may be stored in relation with the geographical objects that originate them (parts of them are precomputed, and on-the-fly combinations are made possible), and what useful data and methods may be stored in addition to the mere shapes of the diagrams's edges.

2.1 Conceptual model

2.1.1. Necessary infra-structure

Basic vector data need some kind of reformulation so that their Voronoi diagram might be associated efficiently:

every component of the geometry, i.e. every intermediary vertex and every pair of successive vertices (i.e. every segment), must have a local identifier (unique in the context of the given object only, not necessarily in the context of the whole database). Such an identified component is called an element in the following.
every segment component must be oriented, i.e. made to show a "left" side and a "right" side.
it helps if the orientation of the segment components is consistent all along the object (i.e. what is on the "left" of a next segment is on the "left" of the given segment). In which case every point component might also be "oriented", as follows: if the angular field of "rightness", as measured from the point between the two successive right sides of the segments, is greater than PI, then the orientation of the point is "right", else it is "left" (see fig. 2. We will not go into the reasons for this "orientation" of points - basically, it consists in marking the contribution of the point to the direction of the curve: when you are on the right side of a segment, when the next segment goes somewhat to the left, the articulation point is rightest indeed, while when the next segment goes somewhat to the right, the articulation point is left indeed).

"Left
Figure 2: "Orientation" of a vertex

2.1.2. Diagram-data association

Relationally speaking, the association of the diagram with the data may be described as follows:

Static relation: A table is stored per object:

Dynamic relation: Upon combination, when several objects need to be processed together, a table is created on the combined diagrams:

In the following,

edges that separate two different objects are called interface edges;
edges within a contour (all of a same side, indicating "inside"), are called internal edges;
edges without a contour (all of a same side, indicating "outside"), are called external edges;

2.2 Attributes per Voronoi edge

To draw a Voronoi diagram is to address the human mind. To make the diagram tractable by the computer, explicit information must be stored in addition to the mere geometric shapes of the edges. Necessary or useful attributes per edge are illustrated in figure 3, and listed in details in sections 2.2.1 to 2.2.10 below. Most of these are necessarily computed, in this or a similar form, during the computation of the diagram itself: no time-consuming extra computation is needed.

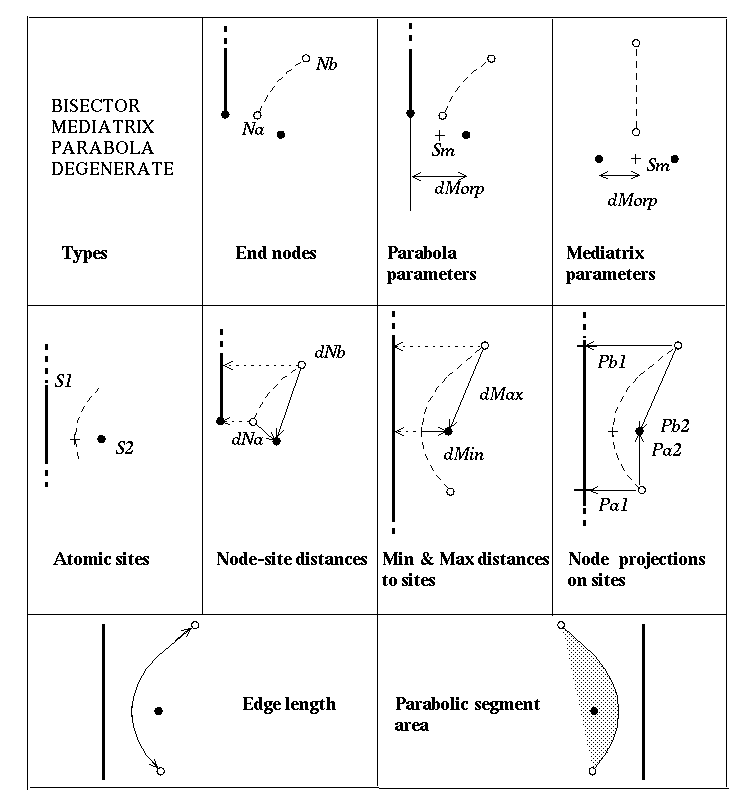
"Illustrations
Figure 3: Attributes per Voronoi edge

2.2.1. Type

Edges may be of the following types:

BISECTOR: Both separated atomic sites are segments.
MEDIATRIX: Both separated atomic sites are points.
PARABOLA: One atomic site is point, the other is segment.
DEGENERATE: Edge at an endpoint of a segment.

2.2.2. End nodes

Na is one of the end node of the edge (i.e. a pair of coordinates), Nb is the other.

2.2.3. Parabola parameters

Two data are stored specifically for an edge of the PARABOLA type:

Sm: pair of coordinates of the vertex of the whole mathematical parabola,
dMorp: distance "morp-hological", i.e. the focal distance (from the focus of the parabola to its directrix)

2.2.4. Mediatrix parameters

Two data are stored specifically for an edge of the MEDIATRIX type:

Sm: pair of coordinates of the middle point between the two separated atomic sites,
dMorp: distance "morp-hological", i.e. half the distance between the two separated sites.

2.2.5. Atomic sites

S1 and S2 are the two atomic sites separated by the edge (the two "elements" introduced in section 2.1).

2.2.6. Node-site distances

dNa = d(Na,S1) and dNb = d(Nb,S1) are the distances from the nodes of the edge to the sites.

2.2.7. Min and Max distances to sites

The Max distance from the edge to the sites is achieved at one of its nodes: dMax = Max (dNa , dNb). The minimal distance, when the edge is a MEDIATRIX or a PARABOLA, may be achieved along the edge: if Sm is on the edge indeed, then dMin(E) = dMorp else dMin(E) = Min (dNa , dNb).

2.2.8. Node projections on sites

Four data are stored:

Pa1 (a pair of coordinates) is the projection of node Na on S1,
Pa2 is the projection of node Na on S2,
Pb1 is the projection of node Nb on S1,
Pb2 is the projection of node Nb on S2.

2.2.9. Edge length

For edges of the BISECTOR, MEDIATRIX or DEGENERATE types, length is the euclidean distance between the two nodes.
For an edge of the PARABOLA type,
u being either of the two unit vectors directing the segment site, and with
ka = min (SmNa . u , SmNb . u),
kb = max (SmNa . u , SmNb . u),
SmNa denoting the vector from Sm to Na, length is:
Le = dMorp/2 . [ Arg sh (kb / dMorp) - Arg sh (ka / dMorp) ]
+ dMorp/4 . { sh [ 2 . Arg sh ( kb / dMorp ) ] - sh [ 2 . Arg sh ( ka / dMorp ) ] }

2.2.10. Parabolic segment area

With the same notations, and introducing:
if ka = SmNa . u then da = dNa and db = dNb
else da = dNb and db = dNa,
the area of a parabolic cap is:
Ar = 1/2 . (kb - ka).(dNa + dNb - dMorp) - 1/3 . [ (db - dMorp/2).kb - (da - dMorp/2).ka ]

Note: Attributes from 2.2.6 to 2.2.10 may be stored as methods, to be evaluated only when triggered.

2.3 Basic formulas

This section describes elementary functions to deal with points on edges and sites, and with distances from diagram to figure. Sections 2.3.1 to 2.3.7 find their illustrations in figure 4 below.

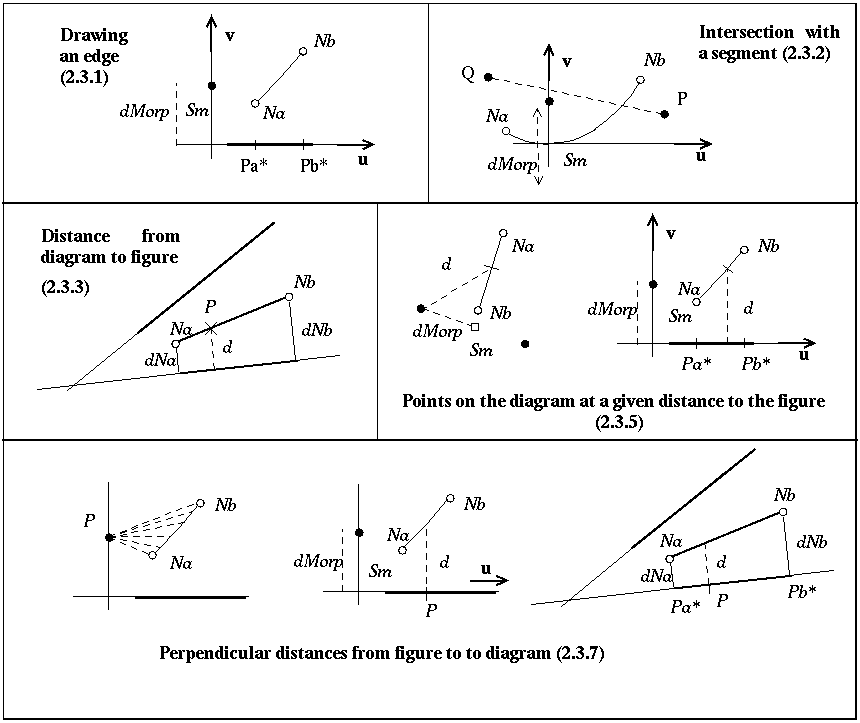
"Illustrations
Figure 4: Illustrations for elementary functions

2.3.1. Drawing an edge

To draw edges of the BISECTOR, MEDIATRIX or DEGENERATE types is to draw line segments. For an edge of the PARABOLA type, with the notations introduced in paragraph 2.2.9, supposing S1 to be the segment site and introducing the unit vector v = Pa1Na / dNa, the relevant portion of parabola to draw has the following (vectorial) equation:
SmM(k) = k . u + k²/(2.dMorp) . v,
k varying in the interval [ ka kb ].

2.3.2. Intersection of a segment with an edge

A segment being superimposed on the diagram, how to compute its possible intersection with a Voronoi edge? The operation is straightforward enough when the edge is of a BISECTOR, MEDIATRIX or DEGENERATE type, and will not be recalled here. When the edge is of the PARABOLA type however, computations are more tricky. With the same notations as before, and introducing the ratio: f = PQ.v / PQ.u, with P and Q the end points of the segment superimposed, the following equation of the second degree must be resolved:
1/(2.dMorp) . k² - f . k + f . SmP.u - SmP.v = 0
Possible roots are to be finally chosen in the interval [ ka kb ].

2.3.3. Distance from a point on the diagram to the figure

The distance from a point P indicated on an edge to the figure is the euclidean distance of this point P with the point site in the case of a MEDIATRIX, PARABOLA or DEGENERATE edge. When the edge is of the BISECTOR type, the distance is:
d = dNa + (dNb - dNa) . d(Na,P) / d(Nb,P).

2.3.4. Edges of the diagram supporting a given distance d to the figure

Simply select edges for which dMin < d < dMax

2.3.5. Points on the diagram at a given distance d to the figure

First select edges supporting distance d.

Then, for an edge of the BISECTOR type: calculate P as:
    NaP = (d - dNa) / (dNb - dNa) . NaNb
For an edge of the DEGENERATE type: calculate P as:
    Pa1P = d / dNa . Pa1Na       (supposing Na the node not coincidental with the segment end point)
For an edge of the MEDIATRIX type: there may be two points.
    compute k = +/- sqrt ( d² - dMorp²)
    and u = SmNa / d(Sm,Na)
    if either value of k is in the interval [ SmNa . u     SmNb . u ] then calculate P as:
    SmP = k . u
For an edge of the PARABOLA type: there may be two points.
    compute k = +/- sqrt [ 2.dMorp.(d - dMorp/2 ) ]
    if either value of k is in the interval [ SmNa . u     SmNb . u ] then calculate P as:
    SmP = k . u + k²/(2.dMorp) . v

2.3.6. Points on the figure for which there is a point on the diagram at a given distance

This merely consists in projecting the points just calculated onto the sites.

2.3.7. Perpendicular distances to diagram from a point on the figure

A point P is given on a site of the figure. From an edge associated to this site, P is considered as the projection of some point(s) along this edge. What is (are) the distance(s) from this (these) point(s) to P?
When P is a point site, the result is: interval [ dMin dMax ]
When P is on a segment site, and the edge of the PARABOLA type, the result is:
d = (SmP . u)² / (2.dMorp) + dMorp / 2
When P is on a segment site, and the edge of the BISECTOR type, the result is:
d = dNa + (dNb - dNa) . d(Pa* , P) / d(Pa* , Pb*)

3. Basic queries

This section is but a catalogue of spatial queries made easier (or indeed, easy) with the structuration described in section 2. For each query, a few words of definition are given, as well as an illustration and a short every-day language algorithm referring to the attributes and methods explained in section 2 (together with the indication of the complexity of this algorithm).

3.1 Convex hull

The convex hull of a figure is the smallest convex contour containing it.
With Voronoi, simply connect successively sites that are separated by infinite edges (dMax = infinite). As there are O(n) Voronoi edges, this is an even smaller O(n) algorithm.

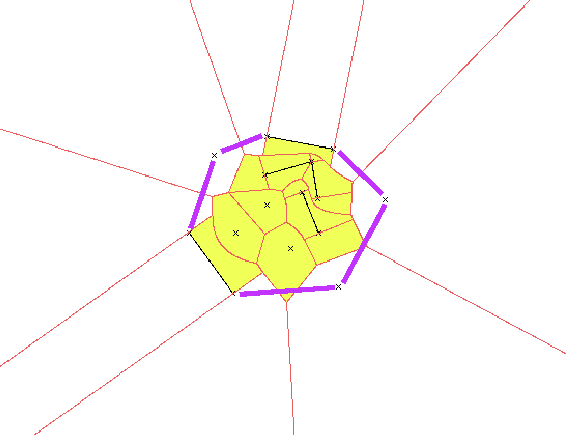
"Convex
Figure 5: Convex hull of a figure (white: infinite cells)

3.2 Skeleton

The skeleton of a contour is the locus of points inside of it that are minimally equidistant to it. With Voronoi, simply select edges within the contour. This may be achieved quickly if the contour is oriented: select BISECTOR, PARABOLA and DEGENERATE edges related to similarly oriented, inside-indicating segments; select also MEDIATRIX edges associated to any point site for which the inside angle (angle between the two connected segments, measured in the inside of the contour) is larger than PI (or, if points are oriented, MEDIATRIX edges associated to inside-indicating points). This is a small O(n) algorithm.

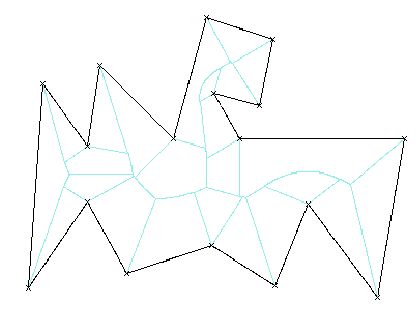
"Skeleton"
Figure 6: Skeleton

3.3 Centroid

A centroid is a point indicated inside a contour, providing some kind of handle to the whole surface. For convex shapes, the centre of gravity is often chosen as the representative centroid. For complex shapes however, the centre of gravity may lie outside of the contour. With Voronoi, any point of the skeleton is a sure centroid, and a refined one is the node of it with the greatest dMax. Which makes a small O(n) algorithm.

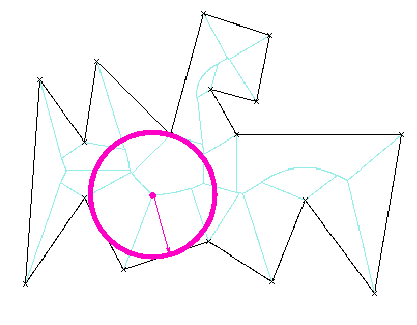
"Centroid"
Figure 7: Centroid

3.4 Frontier

The frontier between two objects (two coasts, two banks etc.) may be defined as the locus of points equidistant from the objects. Simply select interface Voronoi edges.

"Frontier"
Figure 8: Frontier

3.5 Dilation

Dilation in morphological mathematics consists in making an external ball with radius r roll on a contour, and in recording the trace of the center of the ball.
With Voronoi, select external edges that support distance r, and, by sites, points at distance r on them, and connect these points by pair successively by a segment parallel to the segment site, when the two edges relate to a same segment site, by an arc circle centred on the point site when the two edges relate to a same point site (unless the two points of the pair belong to a same edge, in which case there comes a fusion of the inside). This makes a O(n) algorithm.

"Dilation"
Figure 9: Dilation

3.6 Erosion

Erosion in morphological mathematics consists in making an internal ball with radius r roll on a contour, and in recording the trace of the center of the ball.
With Voronoi, select internal edges that support distance r, and, by sites, points at distance r on them, and connect these points by pair successively by a segment parallel to the segment site, when the two edges relate to a same segment site, by an arc circle centred on the point site when the two edges relate to a same point site (unless the two points of the pair belong to a same edge, in which case there comes a rupture of the inside, a discontinuity in the result). This makes a O(n) algorithm.

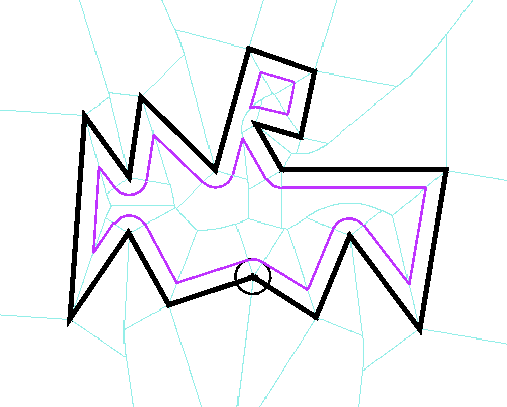
"Erosion"
Figure 10: Erosion

3.7 Closure

Closure in morphological mathematics consists in eroding with radius r2 a dilation with radius r1, with r2 < r1.
Let r' = r1 - r2. With Voronoi, select external edges that support distance r1, and, by sites, points at distance r1 on them. These are called "further points" in the following. Project each further point on either of its sites. On each segment (further point , either of its projection), calculate point P at distance r2 from the further point. When the two sites of the projections are not a segment and one of its end point, connect them by an arc circle with radius r2 centred on the further point. Else, by site, connect successive points P by a segment parallel to the segment site, when the two projections relate to a same segment site, by an arc circle with radius r' centred on the point site when the two projections relate to a same point site (possible intersections & fusions of the resulting contour may occur with this simplified version of the algorithm). This is an O(n) algorithm.

"Closure"
Figure 11: Closure

3.8 Opening

Opening in morphological mathematics consists in dilating with radius r2 an erosion with radius r1, with r2 < r1.
Let r' = r1 - r2. With Voronoi, select internal edges that support distance r1, and, by sites, points at distance r1 on them. These are called "further points" in the following. Project each further point on either of its sites. On each segment (further point , either of its projection), calculate point P at distance r2 from the further point. When the two sites of the projections are not a segment and one of its end point, connect them by an arc circle with radius r2 centred on the further point. Else, by site, connect successive points P by a segment parallel to the segment site, when the two projections relate to a same segment site, by an arc circle with radius r' centred on the point site when the two projections relate to a same point site (possible intersections & fusions of the resulting contour may occur with this simplified version of the algorithm). This is an O(n) algorithm.

"Opening"
Figure 12: Opening

3.9 Hausdorff distance between lines

The Hausdorff distance between two lines A and B is the greater of the two measures:

dH_a>b: greatest of all smallest distances from the points of A to B
dH_b>a: greatest of all smallest distances from the points of B to A

With Voronoi, only a finite set of distances needs investigation. For measure dH_a>b, compute the smallest distances to B from the vertices of A and the intersections of A with the Voronoi diagram of B, and select the greatest of all. (Alt et al. 1993) have shown this to be a O( n . log n) algorithm.

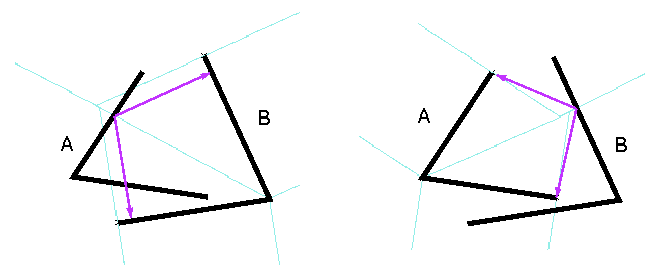
"Hausdorff
Figure 13: The two measures for the Hausdorff distance between lines, from A to B, from B to A

3.10 Hausdorff distance between areas

The Hausdorff distance between two areas A and B is the greater of the two measures:

dH_a>b: greatest of all smallest distances from the points of A to B
dH_b>a: greatest of all smallest distances from the points of B to A

With Voronoi, only a finite set of distances needs investigation. For measure dH_a>b, compute the smallest distances to B from 1/ the vertices of A, 2/ the intersections of the contour of A with the Voronoi diagram of the contour of B, 3/ the nodes of the external Voronoi diagram of B within A; and select the greatest of all. This also is a O( n . log n) algorithm.

"Hausdorff
Figure 14: The two measures for the Hausdorff distance between areas, from A to B, from B to A

3.11 Minimum Spanning Tree

The Minimum Spanning Tree of a set of elements is a non-cycling graph, connecting all elements, the cumulated length of its segments being minimal (compared to other non-cycling all-connecting graphs). Kruskal's algorithm, as exposed in (O'Rourke 1995: p.189), consists in removing segments from a broad set of candidate segments until the MST is constituted. With Voronoi, the initial set of candidates is reduced to a small O(n), as demonstrated in (Hangouët 1998: 160-2): select interface edges for which dMin is different from both dNa and dNb, and use as candidate segment the pair (the point site, its projection on the other point or segment site).

"MST"
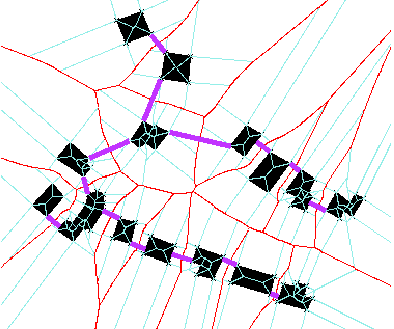
Figure 15: Minimum Spanning Tree on houses

3.12 Geometric waterlining

Waterlining may be defined, in cartography, as the ornemental representation of sea or large rivers in land maps. In (slight) opposition to figurative waterlining (e.g. horizontal lines, or suggestive flow lines, or fishes and waves...), geometric waterlining is mechanically shore- (or bank-) dependent: limicolous points and stretches are made to radiate concentric circles and parallel lines into the water, until they meet other yet simultaneous circles and lines. From the evidence found in some of the Institut Géographique National's collections, it seems that geometric waterlining was in use in French map-making for two hundred years from the mid eighteenth century until after World War II (see e.g. the 1762 "Carte Géométrique du Comté de Nice" and the 1944 edition of the thrichrome edition of the "Nouvelle Carte de France"). In the nineteenth century, the technique was spread worldwide. In his beautiful and important article (Christensen 1999), Christensen describes how waterlining may be revived thanks to the computer, for ornemental drawing yet also for automated spatial analysis.
To draw such waterlines with Voronoi, you merely draw dilations of the land into the water with increasing radii.

"Waterlining"
Figure 16: Geometric waterlining between two banks

Note: It is obvious that on vector data, where polylines make the geometry of the objects, a continuous layering of waterlines and a segment Voronoi diagram are equivalent. The "lack of normalization" for which Christensen reproaches Voronoi diagrams (Christensen 1999: 35) in his otherwise precise and indeed visionary article, if I interpret it correctly, actually addresses the approximation of line data by point data: what in Christensen's paragraph is true of Voronoi diagrams on points (while data come as lines), no longer holds for Voronoi diagrams on segments as exposed in the present paper.

3.13 Bouligand-Minkowski fractal dimension

The Bouligand-Minkowski fractal dimension of a line C is the limit of the expression, when r tends toward 0:
2 - ln A(r) / ln r ,
where A(r) is the area of the "Minkowski sausage" around line C, i.e. line C dilated on its both sides with a radius r.
This on vector data requires intensive computing, which Voronoi somewhat alleviates: for each of the chosen r, the dilation on both sides of the line is computed, then the area of the result. This makes a succession of O(n) computations.

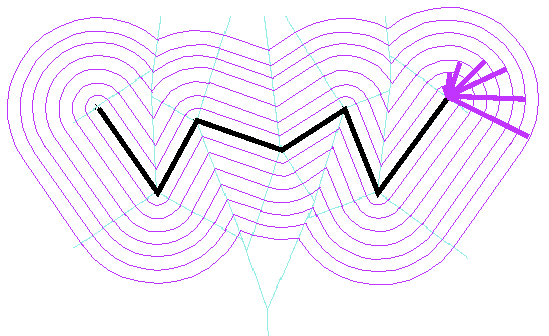
"Fractal
Figure 17: Minkowski sausages of different widths

Note: How to bypass the computation of the area, using the ratio: ln N(r) / ln r, with N(r) number of Voronoi edges with dMin < r , is currently being studied.

3.14 Yet another query...

It seems that away from the big cities - not only from Paris, but also from Amsterdam, Rotterdam and so many others across Europe - one can live better and happier to the world, than in their vicinity... (van Gogh 1889: 532)
In a world where over five sixths of the people are scoundrels, fools or idiots, the rest are forced to live apart, all the more so when they are different - and the greater the distance, the better... (Schopenhauer 1830: 27-8)
Voronoi will help geniuses find isolation: simply select the interface node with the greatest distance to the crowded places...

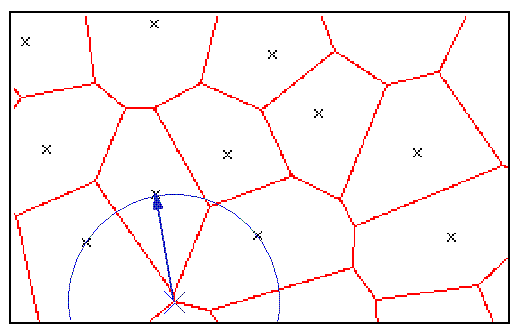
"Isolation"
Figure 18: A happier place

Conclusion

It is well-known that topology (possibly explicitly stored, at least in the awareness we have of it) makes programming spatial queries both more intuitive and more efficacious. The same holds for Voronoi diagrams, and beyond the practical descriptions provided in this paper (which after all may or may not be programmed as such) lies the epistemological argument that the knowledge at least of the properties of Voronoi diagrams on segments, provides one (not omnipotent but in the cartometric domain, reliable) context or paradigm both for apprehending vector geographic data and for programming spatial queries.

References

Alt, H., Behrends, B. and Blömer, J. 1993. Approximate Matching of Polygonal Shapes. Institut für Informatik, Freie Universität Berlin, Report B 93-10, July 1993, available from here

Boissonnat, J.D. and Yvinec, M. 1995. Géométrie algorithmique. Paris: Ediscience international

Christensen, A. 1999. The Revival of a Victorian Art: Waterlining with a Computer. The Cartographic Journal, vol.36 No.1 pp.31-41, June 1999

Computational Geometry Resources

Gold, C. 1999.The Voronoi Web Site

Hangouët, J.F. 1998. Approche et méthodes pour l'automatisation de la généralisation cartographique ; application en bord de ville. Thèse de doctorat, Université de Marne-la-Vallée

Okabe, A. Boots B. and Sugihara K. 1992. Spatial Tessellations. Concepts and Applications of Voronoi Diagrams. Chichester: J. Wiley and sons

Open GIS Consortium. 1999. The OpenGIS^TM Abstract Specification. Topic 1: Feature Geometry (version 4). OpenGIS^TM Project Document Number 99-101.doc

O'Rourke, J. 1995. Computational Geometry in C. Cambridge University Press.

Prisme project

Schopenhauer, A. ca. 1830. Eis Eauton. Paris: Anabase 1992. Translated from the German by Guy Fillion (passage translated from the French by the author)

Strabo. ca. 7bc. Geography, Books 1-2. Translated by Horace Leonard Jones. Cambridge (Ma), London: Harvard, Loeb Classical Library. LCL 49

van Gogh, V. 1889. Letter #598F (to his mother, June 1889) in Correspondance Générale vol.III, Paris: Gallimard, 1990, (passage translated from the French by the author)