The DEM to Mountain Transformation of Zagros Ranges

George Ch. Miliaresis,
Remote Sensing Laboratory, Dept. of Surveying Engineering, National Technical University Athens, 38 Tripoleos Str., Athens 104-42, Greece. E-mail: gmiliar@central.ntua.gr

Abstract

The aim of the present research effort is to implement the DEM to Mountain transformation to Zagros Ranges in Iran, an area of compressional stress. In order to cope with the specific physiographic conditions evident, the Mountain to DEM transformation was modified and the valley pixels were not allowed to participate in the region-growing segmentation process. More specifically, ridge pixels and valley pixels were labeled on the basis of their runoff accumulation value. Then an iterative region-growing segmentation algorithm was applied. During the first iteration, the ridge pixels formed the initial set of mountain pixels while the rest of the pixels formed the current set of non-mountain pixels. In each iteration, if a non mountain pixel satisfied the following three conditions (a) it’s gradient was > 6^o, (b) the pixel was an 8-connected neighbor to the current set of mountain pixels and (c) it did not belonged to the set of valley pixels, then it was flagged as a new mountain pixel and the current set of mountain pixels was updated. The segmentation stopped if no more pixels were added during the current iteration. Then, small isolated islands of mountain pixels that represent either mountain remnants or error-peaks were removed. Additionally, small islands of non-mountain pixels standing on mountaintops and surrounded by mountain pixels were merged to the mountain terrain class. The extracted mountain objects were interpreted to be in accordance to the mountain features interpreted visually from a shaded relief map of the study area.

1. Introduction

Nowadays, the GTOPO30 digital elevation model (DEM) with spacing 30 arc-seconds provides a digital representation of the earth’s relief at a regional scale (http://edcwww.cr.usgs.gov/landdaac/gtopo30/gtopo30.html.). The potential of the DEMs to geomorphometric analysis has been already explained and techniques have being developed in order to automate the interpretation of terrain related features (Pike, 1995; 1999; Miliaresis and Argialas, 2000; Miliaresis, 1999a; 1999b; 2000). Towards this end, a methodology was designed for the extraction of mountains from GTOPO30 DEM (Miliaresis and Argialas, 1999). The methodology was implemented in a study area of size 82,000 km² within the Great Basin where the crust is under tensional forces, thins by normal faulting, and results in an array of tipped mountain blocks that are separated from broad plain basins and producing a basin-and-range physiography (Howell, 1995). On the other hand in Zagros a set of compressional mountain ranges is developed producing a spectacular mountainous physiography due to the collision of the Arabian shield with Iran (Summerfield, 1991). The objective of the present research effort is to implement (and modify, if needed) the DEM to Mountain transformation to an area of compressional stress such as Zagros Ranges.

2. Methodology

First the study area and it’s hypsometric characteristics are introduced. Then the DEM to Mountain transformation is modified in order to cope with the specific physiographic conditions evident in Zagros Ranges. Finally it is implemented and the results are evaluated.

2.1. The study area and the DEM data

The case study was developed for Zagros Ranges (Figure 1) in Iran where the crust shortens and thickens producing a spectacular mountainous physiography due to the collision of the Arabian shield with Iran (Summerfield, 1991). The linear topographic highs represent huge folds (NW-SE anticlines with steeply dipping flanks), that were formed during the Pliocene-Pleistocene orogeny and marked by Southwest-facing topographic escarpments (Berberian, 1995). The geometry of anticlines indicates the existence of basement (high angle) reverse faults that do not cut the overlying folds (Berberian, 1995).

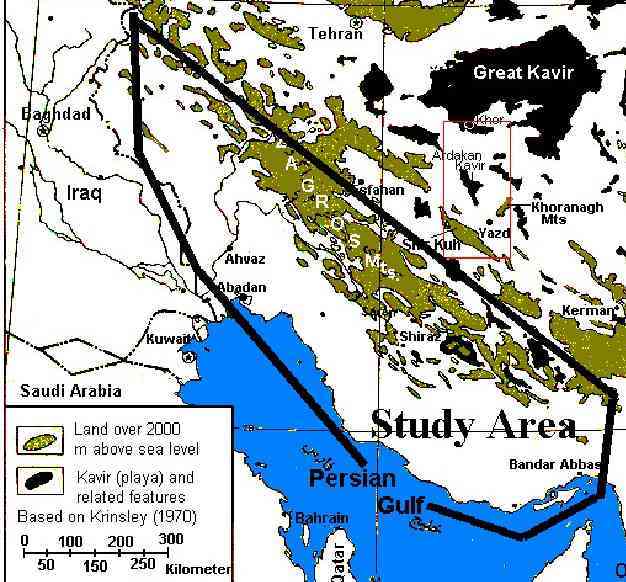
Figure 1. The study area within the Zagros Ranges physiographic zone (Mehrshahi, 1999).

The GTOPO30 DEM of the study area was rectified to a rectangular grid with spacing 926 m and occupied 330,000 km² approximately or 385 775 pixels (Figure 2).

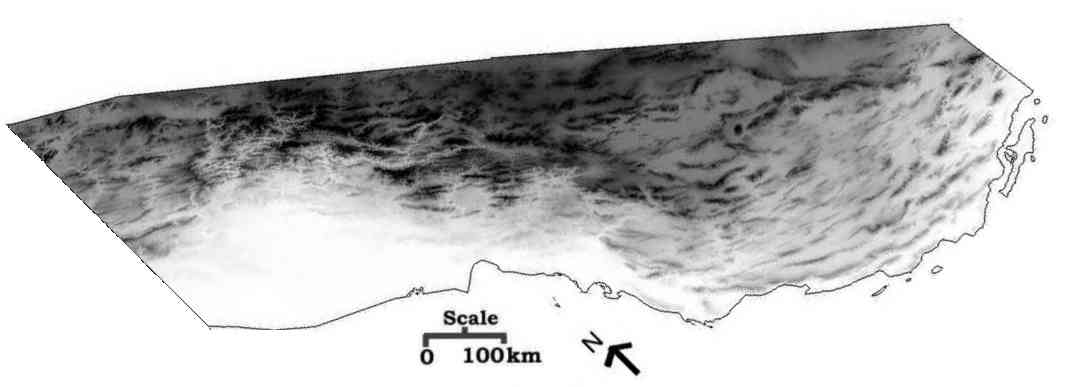
Figure 2. GTOPO30 DEM of the study area. The elevation (1 to 3,000 m) was rescaled to the interval 255 to 0 (the brightest pixels have lowest elevation).

The two elevation profiles (Figure 3) indicate that mountain ranges are built on successively higher baselevels from SE to NW. The The mean elevation is 1,217.3 m with standard deviation 873.2. The study area is higher than the mean land level since the present average elevation of the Earth’s surface is 780 m above sea level (Howell, 1995).

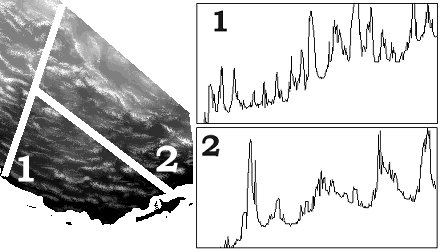
Figure 3. Elevation profiles (1 and 2).

2.2. DEM to Mountain transformation

The DEM to Mountain transformation is actually a region-growing segmentation algorithm that uses the ridge pixels as seeds and a growing criterion that is based on gradient (Miliaresis and Argialas, 1999). Thus gradient and aspect should be computed first. Then the region growing criterion and the ridge should be defined on the basis of the physiographic and geomorphologic conditions evident in the study area.

2.2.1 Gradient and aspect computation

The gradient (Figure 4) and the aspect (Figure 5) were computed on the basis of the Z-operator and the Sobel operator (Miliaresis and Argialas, 1999).

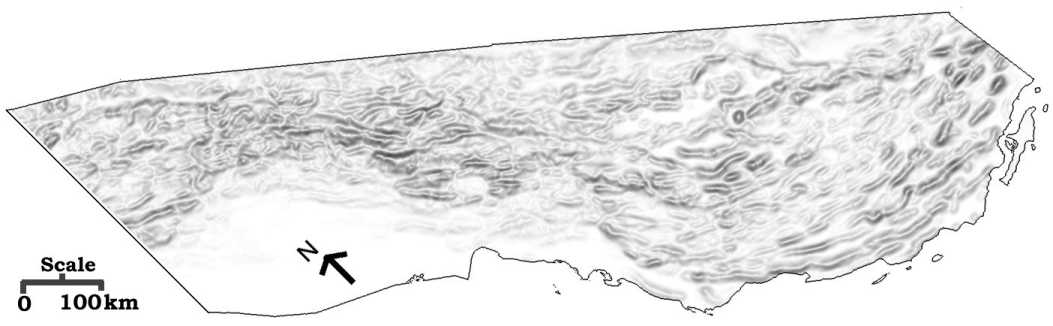
Figure 4. Gradient. The pixels (in the range 0^o to 44^o) were rescaled to the interval 255 to 0 (the brightest pixels have lowest gradient).

Figure 5. Aspect.The aspect was quantified to the eight directions (East=1, Northeast=2, North=3, Northwest=4, West=5, Southwest=6, South=7, Southeast=8) defined in a raster image. Zero labels were used for flat terrain (gradient < 1^o).

2.2.2. Region growing criterion

In the southeast portion of the study area broad gently sloping valleys are observed in between the mountain features. On the contrary in the northwest part more tightly spaced mountain features are observed while narrow, deep, and high sloping valleys are developed in between them. The visual interpretation of Figures 1b and 2a indicate that the mountaintops are rather flat or gently sloping in comparison to the rather steep mountainsides. Training areas statistics indicated that the gradient of mountainsides is greater than 6^oin general. Thus, a region-growing criterion of 6^o degrees would be acceptable (Miliaresis and Argialas, 1999). This is valid for the southeast potion of the study area (broad gently sloping or flat valleys are observed in between the mountains). On the contrary in the northwest part of the study area (narrow deep valleys that slope either to southeast or to northwest with gradient greater than 6^o). In order to cope with this situation, the DEM to Mountain transformation was modified and the region growing the valley pixels were not allowed to participate to the region growing process.

2.2.3. Seeds

In order to proceed the ridge (seeds) and valley pixels (pixels that block the region growing proces) should be identified. The runoff simulation algorithm was used and a single water unit was imported in every pixel of the DEM and traveled in the aspect direction until the edges of the DEM or a pit was reached (Mark, 1984). The water units imported into each pixel were counted and the derived values used to represent the pixel’s runoff (Mark, 1984). A pixel with high runoff value should be labeled either as a ridge pixel (upslope flow) or a valley pixel (downslope flow) depending on the aspect pointing direction. Two thresholds were identified through a trial and error procedure and the pixels with upslope runoff greater than 9 were labeled as ridge pixels (Figure 6) while the pixels with downslope runoff greater than 7 were labeled as valley pixels (Figure 7). A total of 45,031 (11.67 %) pixels were labeled as ridges and 62,327 (16.15 %) pixels were labeled as valleys.

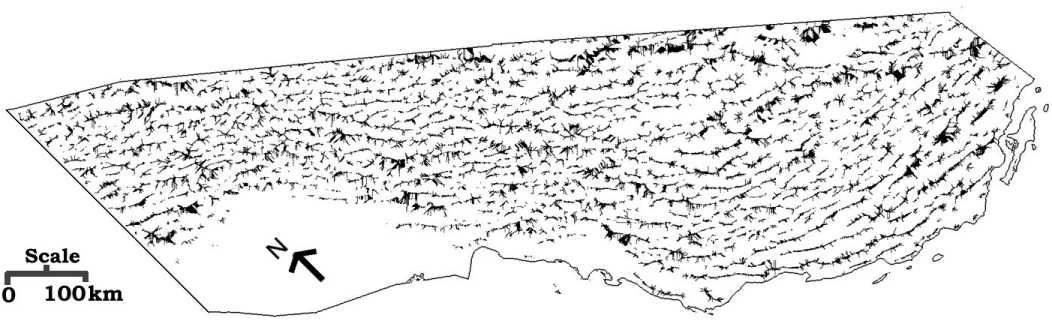
Figure 6. Ridge pixels.

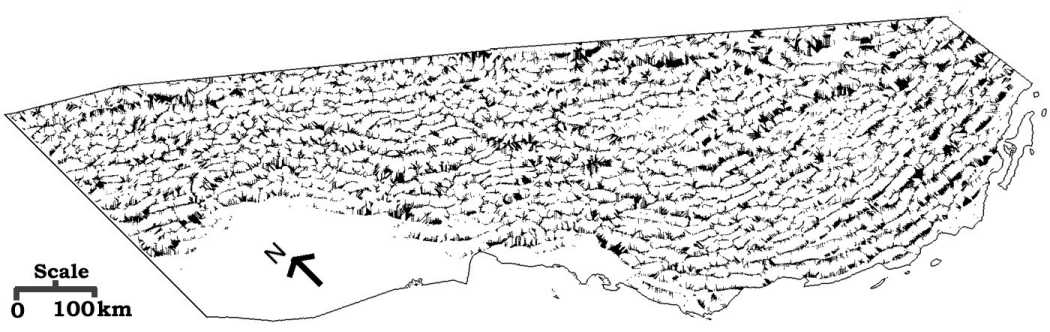
Figure 7. Valley pixels.

2.2.4. Segmentation of mountains

An iterative region growing segmentation was implemented (Pittas, 1993). The ridge pixels formed the initial set of seeds (the current set of mountain pixels during the first iteration, while the rest of the pixels formed the current set of non-mountain pixels). In each iteration, if a non mountain pixel satisfied the following three conditions (a) it’s gradient was > 6^o, (b) the pixel was an 8-connected neighbor to the current set of mountain pixels and (c) it was not labeled as a valley pixel, then it was flagged as a new mountain pixel and the current set of mountain pixels was updated. Note that the 8-connected neighbors are the 9 pixels surrounding the central pixel in a kernel 3*3 (Pitas, 1993). The segmentation stopped if no more pixels were added during the current iteration. Finally, 158,540 (41.01 %) pixels were assigned to the mountain terrain class (Figure 8) after 16 iterations.

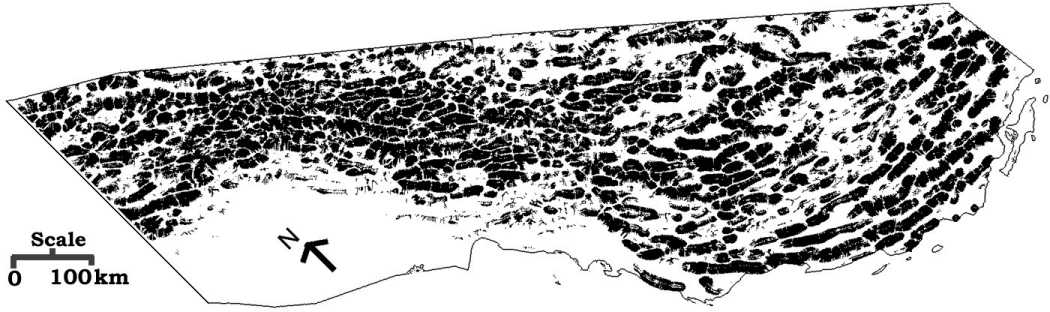
Figure 8. DEM to Mountain transformation. The pixels labeled black represent the mountain terrain class.

The image of the mountain terrain class is quite noisy. More specifically very small isolated islands of mountain pixels were observed that represent either small mountain remnants or artificial error peaks. Additionally small islands of non-mountain pixels were observed occasionally on mountaintops and represent flat or gently sloping areas (gradient < 6^o). In order to correct these artifacts, a connected component labeling algorithm (Pitas, 1993) was applied and both the foreground (mountain terrain class) and the background objects (non-mountain terrain class) were identified and their size was calculated. Then the following processing stages were implemented:

The histogram of the size of the foreground objects was studied and the foreground objects with size smaller than 60 pixels were assigned to the background (5,217 pixels were removed from the mountain terrain class).
The background objects were grouped to two classes. The first one contained a single object with size 229,631 pixels (black region in Figure 3d) while the background objects with size less than 40 pixels formed the second class. The objects of the second class were merged to the mountain terrain class (2,821 pixels were added) since they were enclosed by pixels of the mountain terrain class and they should correspond to the mountaintops.

At the end, 156,144 (40.48%) pixels were found to belong to the mountain terrain class (Figure 9).

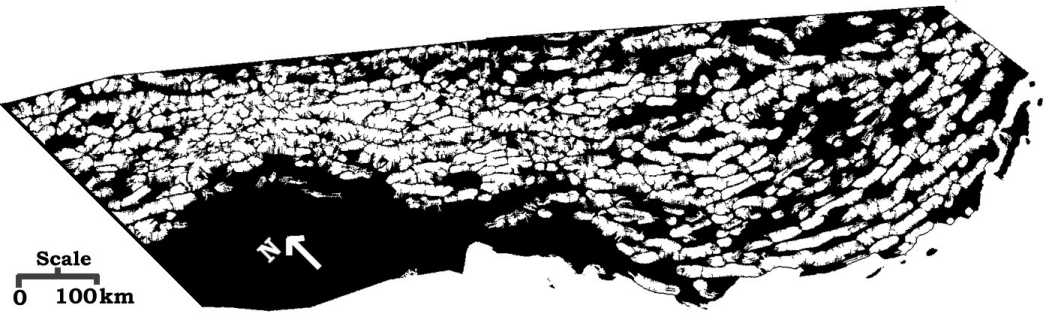
Figure 9.Post-processing of Figure 8. The pixels labeled white within the study area represent the mountain terrain class.

2.3. Evaluation

The evaluation procedure was based on both the visual interpretation of the computer-shaded relief map of the study area and statistical data computed for the mountain and non-mountain terrain classes. Computer shaded-relief maps are a valuable tool for the computer visualization of landscape morphometry, allowing the surface features to viewed in a broad regional context (Reichenbach et al., 1993). The borderlines of the mountain objects were delineated and superimposed on the shaded-relief map of the DEM of the study area (Figure 10). Note that the location of the simulated sun was 30^o above the horizon at NW.

Figure 10. The borderlines (shown black) of the mountains were superimposed on the shaded- relief map of the study area.

In order to assist the interpretation, a hybrid image was created (Figure 11) and the reflectance of the shaded relief map was shown within the regions occupied by the mountain objects while the background was depicted white. It was observed that (a) the majority of the mountain features that were interpreted from the shaded-relief map, were also extracted by the DEM to Mountain transformation and (b) the algorithm followed their shape. Exceptions were some very small mountain objects observed mainly in SW that were erased during the post-processing stage.

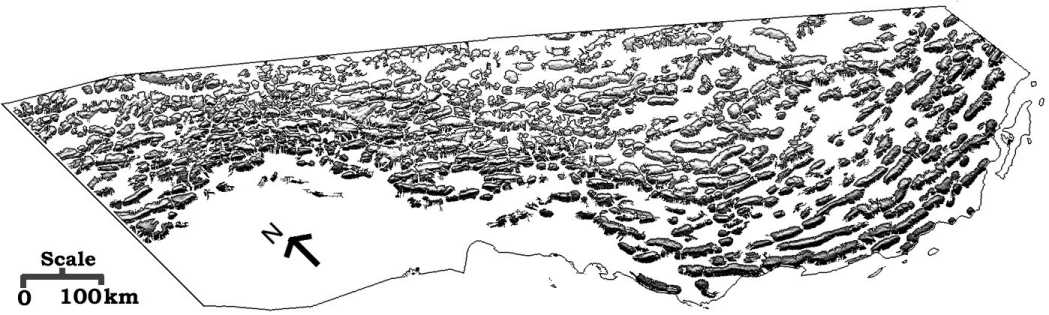
Figure 11. The reflectance of the shaded relief map was depicted within the mountain objects while the background was depicted white.

3. Concluding comments

The DEM to Mountain transformation was modified in order to cope with the more tightly spaced mountain objects in the Zagros Ranges continent to continent coalition morphotectonic context. More specifically region growing was not allowed for the pixels that were labeled as valley pixels. In the near future more accurate DEMs of higher spatial resolution will be available allowing more detailed investigations. For example one could use, digital terrain data from the Space Shuttle radar interferometric topography mapper (SRTM). SRTM was designed to acquire digital elevation maps of all regions of earth surface between 54 S and 60 N latitude with 16 m absolute vertical height accuracy

References

Berberian, M., 1975. Master "Blind” Thrust Faults Under the Zagros Folds: Active Basement Tectonics and Surface Morphotectonics. Tectonophysics, Vol. 241, pp. 193-224.

Howell, D., 1995. Principles of Terrane Analysis - New Applications for Global Tectonics, Chapman and Hall, London.

Mark, D., 1984. Automated detection of drainage network from digital elevation models. Cartographica, Vol. 21, pp. 168-178.

Mehrshahi, Daryoushm, 1999. Iranian Deserts. http://www.geocities.com/CollegePark /Square/2077/home2.html

Miliaresis, G. and D. Argialas, 1999. Segmentation of Physiographic Features from the Global Digital Elevation Model/GTOPO30. Computers & Geosciences, Vol. 25, No. 7, pp. 715-728.

Miliaresis, G. and D. Argialas, 2000. Extraction and Delineation of Alluvial Fans from Digital Elevation Models and Landsat Thematic Mapper Images. Photogrammetric Engineering & Remote Sensing, [ to appear in August 2000 ]

Miliaresis, G., 1999a. A region-growing algorithm for the segmentation of alluvial fans from digital elevation models. Proceedings, 1^st International Symposium on Imaging Applications in Geology (GeoVision 99). Liege, Belgium, pp. 189-192.

Miliaresis, G., 1999b. Automated segmentation of alluvial fans to regions of high to intermediate flood hazard from Landsat Thematic Mapper imagery. Proceedings, 2^nd International Symposium on Operationalization of Remote Sensing. Enschede-ITC, The Netherlands, (6 pp.).

Miliaresis G., 2000. Segmentation of Alluvial Aprons from the USGS Digital Elevation Models with Spacing 2-Arc Seconds. Proceedings, RGS-IBG 2000, Session on Surface Modeling in Geography, Sussex, (U.K.) January 4-7.

Pike, R., 1995. Geomorphometry-Process, Practice and Prospects. Zeitshcrift f. Geomorphologie N.F. suppl. Bd., Vol. 101, pp. 221-238.

Pike, R., 1999. A Bibliography of Geomorphometry, the Quantitative Representation of Topography-Supplement 3 (Open-File Report 99-140), U.S. Geological Survey, Menlo Park.

Pitas, I., 1993. Digital image processing algorithms, Prentice Hall, London.

Reichenbach, P., R. Pike, W. Acevedo and R. Mark, 1993. A new landform map of Italy in computer-shaded relief. Anno LII - Bolletino Di Geodesia E Scienze Affini, Vol. 1, pp. 21-44.

Summerfield, M., 1991. Global Geomorphology, Longman Group, Essex.