Return to GeoComputation 99 Index

Estimating subpixel geospatial features

Henry Berger and James Shine
U.S. Army Topographic Engineering Center, 7701 Telegraph Road, Alexandria, VA 22315-3864 U.S.A.
E-mail: hberger@usace.army.mil
E-mail: jshine@tec.army.mil

Abstract

This paper describes a method for estimating subpixel geospatial features in special circumstances. These come from spatial imagery when the details of these features are too small or have spatial or ground-compositional or ground-level altitude nonuniformities that vary so rapidly that normal pixel-level spatial data acquisition from a variety of imaging techniques mentioned below has insufficient resolution to determine these special features accurately. Despite these limitations, ways have been found to estimate the mini-images that might have been seen within the instantaneous-field-of-view (IFOV) viewed by the usual pixel that represents single numerical values within the wavelength bands of interest. This also seems to lead naturally to the tagging of clusters of otherwise nondescript pixels. We feel this may help reduce the identification difficulty in areas such as the correspondence problem of conventional photogrammetry and possibly other areas.

1. Introduction

Mark Williams has written a solid account of different methods of obtaining geospatial data from various sorts of imagery, including his own, for "Spatial Data Acquisition from Motion Video" (Williams, 1996). His discussion ranges over conventional photogrammetry summarizing the basic methods of: interactive methods, target based methods and fully automatic methods. He briefly discusses the three main areas of computational stereo: human visual systems, robot systems and image metrology. He then briefly introduces shape from motion and monocular methods such as shape from shading and shape from contour. Other methods are briefly mentioned as well.

Williams makes an incisive comment on all these methods that bears repeating before discussing the special domains the authors investigate:

"All of the methods described above have proven to be successful in particular cases. All have constraints, however, including adding reference to the scene, controlling the lighting or making assumptions about the reflective properties of the surface."

This comment will apply equally in the work we are to describe.

The November 1998 Optical Engineering article, "Data Analysis Systems for Films," by D. Zhang, et al., on subpixel estimation for sequential spatial imagery of moving objects recorded on film, then converted to digital imagery, uses a correlation technique to better locate a small number of key spatial points in the image (Zhang, 1998). The intent here was for high-speed photography. A method of correlation matching is described, based on previous work. Here subpixel methods are described for locating identical points within a sequence of neighboring sequential images. In light of the comments quoted above, one must wonder if the kinds of problems, such as the nonuniform illumination of individual sensing elements, and inferring radiance from measured irradiance in the presence of such nonuniform illumination, will set serious bounds on the results of this kind of approach.

The current paper describes a method that estimates, for the region within each pixel / IFOV, spatial coordinates of effective centers-of-gravity of the optical illumination based on illumination data from neighboring pixels/IFOVs. The Williams paper discusses expressions such as "pixel intensities" and "subpixel coordinates." This paper will discuss the meaning of these words under conditions such as:

(1) the objects or structures are not much larger than a pixel size; (2) the topography of the ground surface has relative fine gradations; and (3) the reflectance changes relatively rapidly because of almost abrupt changes in ground compostion or because the ground altitude abruptly rises or drops.

Ordinary sized objects appear small when circumstances require considerable distances between imager and object or the imaging is done from a low flying plane. On the other hand some interesting objects are inherently small. Abrupt changes in ground composition are ordinary when strips of cultivated land terminate, and large rock formations end. Rapid changes in ground level can occur in hills, old mine shafts, and in other circumstances.

2. Nonuniform illumination

When these circumstances occur, each of the detectors or elemental film elements recording the image are illuminated in an unknown nonuniform way, and since each element is sensing a different portion of the scene, the unknown variations vary from element to element. The significance for the image recorded is two fold. First, these elements of the imaging sensor records the average power by which it was illuminated, i.e., a single numerical value, with no structure of the nonuniformity left. This has two impacts. First this acts in ways such as noise, blurring the image, reducing the contrast and the resolution as described by McKenna (in Berger, 1997).

The second aspect is that this apparent noise contains information about the fine details of the image of interest if only we knew how to extract it. The second element of significance is that these sensing elements measure irradiance (E), while it is the radiance (L) inferred from them that is used to construct the image. The radiance and irradiance are related by the mathematical derivative [2]

L = dE/dW (1)

where W is defined as the projected solid angle. The irradiance measures all separate "streams" of power upon the detecting surface no matter what the angle of incidence. But in the more formal theory, the radiance, has some direction associated with it. While this paper will refer to previous ones for much of the mathematical details, it should at least be clear at this point that inferring L from the measurements of E from a few sensing elements that are illuminated in an unknown nonuniform manner, is not a trivial problem.

What is commonly done is to assume that the illumination of the individual sensing element is uniform and so from the integral form of (1) it is straightforward that

L = Eu W (2)

where Eu is either the assumed, but initially unknown, uniform value of illumination or, if not uniform, represents some average value. It is normally assumed to be a uniform value.

This paper will present a way to estimate a mini-image in place of each pixel’s single numerical value for a given wavelength band. The accuracies of these estimations depend on the magnitude of the other types of image noise present. The mini-image will estimate those features that would have been seen in the IFOV of the object or ground surface viewed by that pixel. Such mini-images may be helpful in the crucial correspondence problem in photogrammetry as well as elsewhere.

3. Neighborhoods of pixels

For objects whose boundaries reside solely within a single pixel the methods of this discussion are of little use; however, quite often even small objects and seemingly abrupt terminations spread out through several neighboring pixels although perhaps at low levels. Surprisingly, even at low levels, trends in nonuniform illumination can be estimated accurately, as will be seen. These trends can be used to estimate variations within the IFOV of a pixel. As an example, consider the one-dimensional block of pixel values whose intensities are shown in Figure 1:

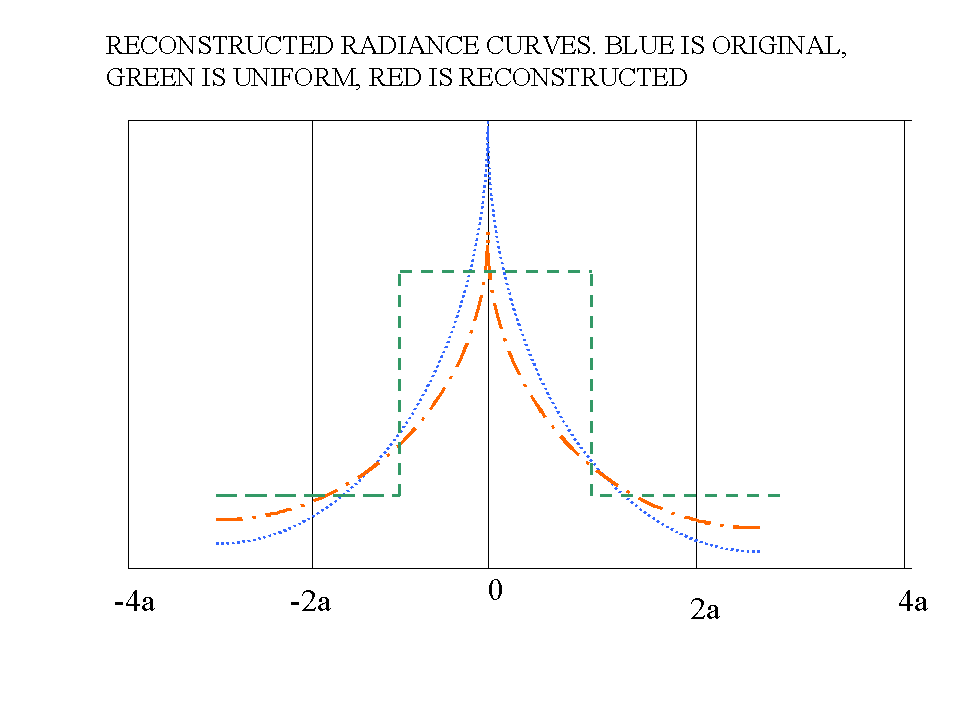
Figure 1.

In Fig. 1, A illustrates a curve representing an assumed nonuniformly illuminating radiance, B illustrates the pixel array such that a curve would generate on an imaging sensor, and C represents the reconstruction of the curve that the methods to be discussed can produce. It should be clear that the original curve hidden in the dot is reproduced quite accurately. When changes from pixels to pixels are not great, one’s confidence is that some sort of extrapolation using the pixel of interest at its core will produce a reasonable curve within the IFOV of any one pixel. Of course the accuracy will depend on how it is executed, and as seen in Figure1, the accuracy can be quite good with modest tools. The correspondence problem in conventional photogrammetry is often finally resolved with a least-squares analysis of pixel intensity. How different would our procedures for correspondence be if different shapes could be made out for most of the pixels of interest with varying intensities within each pixel?

4. Optical centers of gravity for pixels

Sky-viewing optical trackers have been able to locate single targets to accuracies within 1/100 of a pixel in a four contiguous pixel grid embedded within grids of pixels of far greater numbers as mentioned by (Berger, 1998). This may be the first time centers-of-gravity surface-viewing systems for ground viewing optical imagers have been considered to construct local coordinate systems. They are the region within each pixel / IFOV, spatial scene and are partially based on illumination data from neighboring pixels / IFOVs.

These, in turn, form the basis for setting up local coordinate systems in which interpolation based upon data from neighboring sensing elements are used to estimate the illumination intensity at each spatial point within each IFOV for all of the detectors or film element surfaces in the array.

In order to do all for a single sensor element, we infer trends from neighborhoods of detectors local to and encompassing the one of interest. To do this data, trends are inferred from neighborhoods of detectors. The establishment of a primary axis is at first problematic. But the center of each pixel presents itself as a convenient starting point and one that initially allows some homogeneity; thus, we initially associate with this center the measured pixel intensity (power-per-unit area (irrradiance) times the effective sensor area). This irradiance can be converted to a radiance value using a method that emulates the derivative definition operationally by the taking the equivalent of a limit using a nested set of enveloping neighboring sensing elements (as discussed by Berger, 1997). A less accurate approach is to use the equivalent average result derived in Appendix B, below. Various forms of interpolation can then be used to connect up these centers in a manner yielding a unique value of irradiance I(Æ ) at each point along the network of interconnected centers. To some extent the preceding may seem arbitrary, but there is a discipline the ith set of interconnections must adhere to and that is given (in one-dimension) by the fundamental data integral constraint for energy as discussed by (Berger, 1998).

E_i = ò K_i I_i(Æ ) dÆ (3)

A: AN OUTLINE OF THE BASIC RADIOMETRIC PROBLEM

----------------------------------------------------------------------------------------------------------------------

PROBLEM: MEASUREMENTS PRODUCE THE IRRADIANCES , i.e. NUMBERS (E_O). WE

NEED TO INFER FOR EACH E_O A RADIANCE, A FUNCTION L (Æ , b ) FOR THE

INDIVIDUAL DETECTORS IN AN ARRAY. L( Æ ,b )s ARE USED TO FORM THE IMAGE.

----------------------------------------------------------------------------------------------------------------------

C. CENTROID

-----------------------------------------------------------------------------------------------------------------

ò J L (J ) dJ

<J > º ---------------------- (6)

ò L (J ) dJ

6. Conclusions

This paper addresses concerns in special circumstances; however, the results may find uses outside these areas such as reducing ambiguity in the correspondence problem in standard photogrammetry. The area of consideration in this paper deals with cases where spatial data, acquired through imaging, involves objects that may be little larger than the basic pixels themselves; where the reflectance varies rapidly because the composition of the object varies almost abruptly; or where the altitude of the ground surface suddenly varies rapidly. There are two circumstances here that may be most fundamental in these situations. The first may be the presence of highly nonuniform illumination of the instantaneous-field-of-view (IFOV) of the individual sensing elements. The second is that the image is composed of radiance, but the sensing elements measure irradiance not radiance, and the radiance must be inferred in the presence of the highly nonuniform illumination. Methods in the early stages of development have been devised to deal with these problems with some considerable success achieved.

References

Berger, Henry and E.H. Bosch, 1997. "Processing Irradiance Data in th Field-of-View Domain," Proceedings of ISSSR97.

Berger, Henry, E.H. Bosch, and E. Simental, 1998. "Correcting Radiance Data for Randomly Occurring Nonuniform Illumination of Individual Detectors in Arrays," Proceedings of SPIE, Vol. 3372, Algorithms for Multispectral and Hyperspectral Imagery IV, 13-14, pp. 158-165.

Williams, Mark, 1996. "Spatial Data Acquisition from Motion Video," Proceedings of GeoComputation 1996, Volume II, pp. 857-875.

Zhang, Dongsheng and X. Zhang, 1998. "Data Analysis System for Film", Optical Engineering, pp. 2,914-2,917.