Return to GeoComputation 99 Index

An improved algorithm for calculating the perimeter and area of raster polygons


Steve Prashker
Department of Geography, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario, Canada K1S 5B6
E-mail: steve_prashker@carleton.ca

1. Introduction

Geographic Information Processing and Digital Cartography, by their very nature, employ digital techniques and sophisticated algorithms for analyzing and displaying digital geographic data. One assumes that the software one uses contains methodologies and algorithms to solve the particular geographic or spatial problem at hand, accurately and precisely. We implicitly have confidence in the implementation of these algorithms, and generally assume that the results produced by these GIS are as accurate as the developers of the software intended them to be. We put faith in their judgement for the selection and implementation of various algorithms for solving, in this context, spatial geographic problems. However, sophistication of software and accuracy of results may not go hand in hand. A simple case in point is the calculation of the perimeter and area of a polygon, within a raster data structure. This calculation seems simple enough, but in extreme cases, most GIS systems produce errors of up to 40% for the perimeter calculation, and up to 10% for area calculations. This paper will examine the typical algorithms used for calculating the perimeter and area statistic, and will present an improved algorithm that produces much less error,

2. Traditional methods

The structure of a spatial data set determines the type of algorithms employed to analyze the data. In a GIS, the two main data structures are raster and vector, and each has properties suitable for solving problems unique to their data structure. Each has their advantages and disadvantages for solving these geographic problems, and algorithms that are simple to implement in a raster environment may be difficult to implement in a vector environment, and vice versa. Traditional methods of calculating the perimeter and area of a polygon, in raster and vector format, will expose the weakness of the raster calculation.

3. Vector format algorithms

In a vector data structure, the perimeter of a polygon is easily and accurately calculated using the Pythagoras formula. The distance between two vector coordinates, x1,y1 and x2,y2 is given by the formula

For a closed polygon containing N vertices (where xN=x1 and yN=y1), a simple summation of the lengths of all the edges of the polygon will result in the perimeter of the polygon. Stated as a formula,

The area of a vector polygon is also easily computed, using several techniques. Using the Trapezoidal method, each side of the polygon forms a trapezoid with the X axis (see Figure 1).


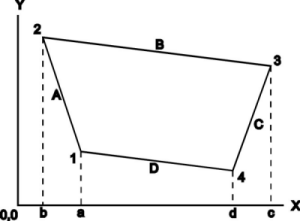
Figure 1. Vector polygon with each side subtending a trapezoid

The area of a trapezoid subtended by polygon side A, from coordinate x1,y1 to x2,y2 is

This is effectively the width times the average height, and gives the area of an equivalent rectangle. For a closed polygon containing N vertices (where xN=x1 and yN=y1), a simple summation of the areas of all the subtended trapezoids of the polygon will result in the total area of the polygon, assuming a clockwise directed polygon. Stated as a formula,

4. Raster format algorithms

In raster space, the algorithms for computing perimeters and areas of polygons (or raster areas, contiguous areas of common value) are generally quite simplistic, and not as precise as the vector methods. For the area calculation, the numbers of pixels contained within the polygonal area are counted. The pixel size is a known quantity, so the area of a pixel is also known. Multiplying the number of pixels by the area of one pixel results in the area of the polygon. For perimeters of raster polygonal areas, a more complex algorithm is employed. All edges of the polygonal region (an edge of a raster polygon exists when a pixel of the raster polygon has an adjacent pixel of a different value) are determined and counted. Multiplying the number of edges by the length of the side of a pixel results in the perimeter of the polygonal area. The difficulty with this technique is the inherent problem of the raster data structure – aliasing in the representation of non-vertical or non-horizontal lines.

When a vector map is rasterized for use within a GIS, the horizontal and vertical sections of boundary lines are converted into straight rows or columns of pixels. However, the other ‘diagonal’ sections of lines are converted into ‘stairstep’ like lines, using raster pixels, which attempt to follow the straight vector lines. This results in aliasing, that jagged look to the lines due to the pixelation effect. The finer the resolution (i.e. the smaller the pixel), the less apparent is the aliasing. Nevertheless, this aliasing causes an overestimation in the number of edges used to represent the boundary of a region in raster space. When a diagonal section of the perimeter of the polygon is represented in raster space, typical algorithms count the two exposed edges of the pixel as contributing to the perimeter, or two times the length of the side of the pixel. A more accurate calculation would count the diagonal distance across the pixel, or root 2 times the length of the side of the pixel. Figure 2 demonstrates the aliasing problem in the raster representation of vector objects. This simplicity of current algorithms, which ignore the significance of the aliasing problem, contributes to the errors of the perimeter and area statistic. By experimentation, using the nine square raster file described later, it was proven that IDRISI, EPPL7, PCI, ArcView and SPANS GIS all implement the same simple algorithms, since the results of their perimeter and area calculations were identical among them. Because of this, any subsequent reference to IDRISI is interchangeable with any of the above mentioned GIS systems. This simple experiment can easily determine if these simple algorithms are implemented in any GIS system.

Figure 2. A rotated square and its rasterized equivalent

5. Improved algorithm

The algorithm presented here attempts to compensate for the aliasing problem by adjusting for diagonal sections of polygon boundaries. To determine the appropriate contribution of an edge pixel to the perimeter, a scheme was devised to determine edge pixels (or pixels with edges bounding on unlike pixels), and their corresponding perimeter contribution. A 3x3 pixel matrix, or moving window, was defined that would represent every combination of up to 8 like pixels surrounding the centre pixel. Each of the 8 surrounding pixels would have a unique position code, as shown in Figure 3. Summing these codes, when an adjacent pixel has the same value as the central pixel, would result in a number between 0 and 255, or one of 256 unique pattern values. Figure 4 shows the 256 different surround patterns in sequential order. Each unique pattern value has a perimeter value associated with its unique pattern, and, by examining each pattern, an appropriate perimeter value was selected for each pattern. A pattern could have one of six perimeter values (1, 2, 3, 4, 1.414 or 2.828), depending on the pattern shape with respect to the central pixel. A pattern with a perimeter value of 1 has one exposed edge on the polygon boundary; a perimeter value of 3 has three exposed edges on the polygon boundary; a perimeter value of 1.414 (square root of 2) represents a diagonal line through the pixel; a perimeter value of 2.828 has two diagonal lines through the pixel. Figure 5 shows the pattern values and their associated perimeter values.

The algorithm procedure would systematically apply the moving window at every pixel, compute the surrounding pixel pattern value, and determine the associated perimeter value. Then, for each class of pixel in the raster image, a running total of perimeter values would be accumulated. Once all pixels in the raster image are processed, the running total for each pixel class is multiplied by the length of a pixel edge, resulting in the perimeters of all the polygons (areas) in the image.

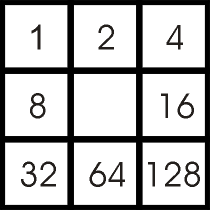
Figure 3. The 3x3 pixel matrix moving window, showing pixel position codes

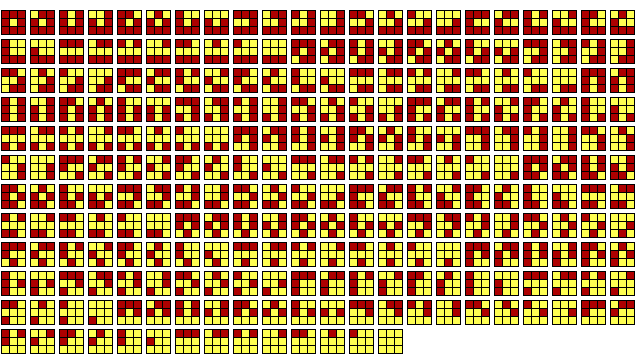
Figure 4. The 256 unique pixel surround patterns

Pattern Value Codes and Associated Perimeter Contribution Value

Code Perimeter Code Perimeter Code Perimeter Code Perimeter Code Perimeter Code Perimeter Code Perimeter Code Perimeter
0 4 32 4 64 3 96 1.414 128 4 160 4 192 1.414 224 2.828
1 4 33 4 65 3 97 1.414 129 4 161 4 193 3 225 3
2 3 34 3 66 2 98 2 130 3 162 3 194 2 226 2
3 1.414 35 1.414 67 2 99 2 131 3 163 3 195 2 227 2
4 4 36 4 68 3 100 3 132 4 164 4 196 1.414 228 3
5 4 37 4 69 3 101 3 133 4 165 4 197 3 229 3
6 1.414 38 3 70 2 102 2 134 1.414 166 3 198 2 230 2
7 2.828 39 3 71 2 103 2 135 3 167 3 199 2 231 1.414
8 3 40 1.414 72 2 104 2 136 3 168 1.414 200 1.414 232 1.414
9 1.414 41 2.828 73 1.414 105 1.414 137 3 169 3 201 1.414 233 1.414
10 2 42 1.414 74 1 106 1 138 2 170 2 202 1 234 1.414
11 2 43 1.414 75 1 107 1 139 2 171 2 203 1 235 1
12 3 44 3 76 2 108 2 140 3 172 3 204 2 236 2
13 1.414 45 3 77 2 109 2 141 3 173 3 205 1.414 237 1.414
14 1.414 46 1.414 78 1 110 1 142 2 174 1.414 206 2 238 1
15 1.414 47 1.414 79 1.414 111 1 143 2 175 1.414 207 1 239 1
16 3 48 3 80 2 112 1.414 144 1.414 176 1.414 208 2 240 1.414
17 3 49 3 81 2 113 2 145 3 177 3 209 2 241 2
18 2 50 2 82 1 114 1 146 1.414 178 2 210 1 242 1.414
19 1.414 51 2 83 1 115 2 147 1.414 179 1.414 211 1 243 1
20 1.414 52 3 84 1.414 116 1.414 148 2.828 180 3 212 1.414 244 1.414
21 1.414 53 3 85 2 117 1.414 149 3 181 3 213 2 245 1.414
22 2 54 2 86 1 118 1 150 1.414 182 2 214 1 246 1
23 1.414 55 2 87 1.414 119 1 151 1.414 183 1.414 215 1 247 1
24 2 56 2 88 1 120 1 152 2 184 2 216 1 248 1
25 2 57 2 89 1 121 1.414 153 2 185 2 217 1 249 1
26 1 58 1 90 0 122 0 154 1 186 2 218 0 250 0
27 1 59 1.414 91 0 123 0 155 1 187 1 219 0 251 0
28 2 60 2 92 1 124 1 156 2 188 2 220 1.414 252 1
29 2 61 2 93 2 125 1 157 2 189 1.414 221 1 253 1
30 1 62 1 94 0 126 0 158 1.414 190 1 222 0 254 0
31 1 63 1 95 0 127 0 159 1 191 1 223 0 255 0

Figure 5. The 256 pattern values and their associated perimeter values

6. The experiment

To observe the improvement in accuracy of the computed perimeters and areas, two tests were performed.

6.1 Perimeter Test 1.

Nine vector squares, 100 units on a side, were created, each rotated by five-degree increments, from 5 to 45 degrees, to show the effects of increased aliasing on the square boundaries. Elementary geometry shows that each square has a perimeter of 400 units, and an area of 10000 square units, regardless of its orientation in vector space. The nine squares were then rasterized in the IDRISI GIS, at 5 different resolutions (75, 150, 300,600 and 1200 pixels for an image 600 units square, or 8,4,2,1 and 0.5 units/pixel respectively), and the perimeter and area of each rasterized square was computed and compared to its vector equivalent. The improved algorithm was also used to calculate the perimeters and areas of the rasterized squares. Figure 6 shows the nine squares superimposed on their rasterized versions. The results of the IDRISI perimeter calculation, including average error from the exact vector values, is shown in Figure 7. As can be seen, errors of up to 40% can result from area boundaries containing severe aliasing, such as the square rotated by 45 degrees. Figure 8 graphically shows, as rotation angle increases, aliasing increases, and corresponding error increases asymptotically to a maximum of about 38%, regardless of resolution. The results of the improved algorithm perimeter calculation, including average error from the exact vector values, are shown in Figure 9. As can be seen, error has been significantly reduced to about 8.4% for the most severely aliased square. Figure 10 graphically shows the error of the perimeter calculation, at 5 different resolutions, using the improved algorithm. A maximum occurs at about 11.5%.

Figure 6. Test 1 – Nine rotated squares superimposed on their raster equivalents
  Resolution - Perimeter Values
using IDRISI		          
Rotation
in Degrees		 75x75 150x150 300x300 600x600 1200x1200 Vector
5 416 416 432 432 432 400
10 480 448 464 464 464 400
15 480 480 496 488 488 400
20 480 512 512 512 512 400
25 544 512 528 528 532 400
30 544 544 544 544 548 400
35 544 544 544 552 556 400
40 544 576 560 560 564 400
45 544 544 560 560 564 400
             
  Resolution - %Error
using IDRISI		          
Rotation
in Degrees		 75x75 150x150 300x300 600x600 1200x1200  
5 4 4 8 8 8  
10 20 12 16 16 16  
15 20 20 24 22 22  
20 20 28 28 28 28  
25 36 28 32 32 33  
30 36 36 36 36 37  
35 36 36 36 38 39  
40 36 44 40 40 41  
45 36 36 40 40 41  

Figure 7. Table of IDRISI perimeter values for nine rotated squares, at five different resolutions
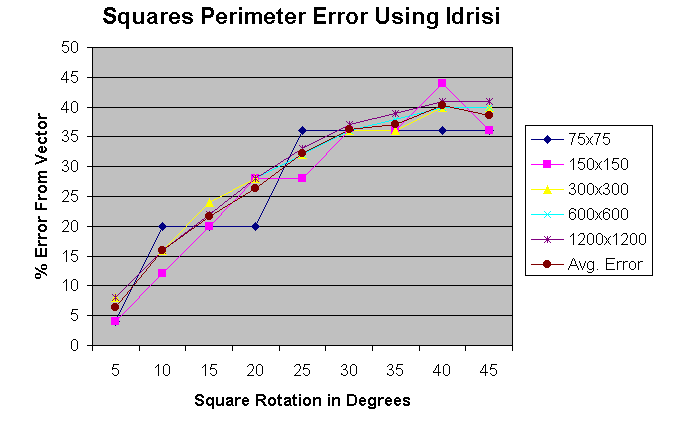
Figure 8. Chart of IDRISI perimeter error for nine rotated squares, at five different resolutions
  Resolution - Perimeter Values using
Improved Algorithm		          
Rotation in
Degrees		 75x75 150x150 300x300 600x600 1200x1200 Vector
5 393.63 382.45 409.63 409.63 408.24 400
10 435.27 403.27 408.09 416.47 415.08 400
15 412.90 412.90 415.31 418.11 416.71 400
20 412.90 422.54 411.35 416.95 416.95 400
25 409.81 411.36 414.80 413.38 412.58 400
30 426.68 398.62 409.81 407.01 406.82 400
35 409.81 398.62 387.44 392.65 395.25 400
40 365.08 385.89 381.08 381.08 383.68 400
45 381.95 353.89 364.30 364.30 366.91 400
             
  Resolution - %Error using
Improved Algorithm		          
Rotation in
Degrees		 75x75 150x150 300x300 600x600 1200x1200  
5 1.59 4.39 2.41 2.41 2.06  
10 8.82 0.82 2.02 4.12 3.77  
15 3.23 3.23 3.83 4.53 4.18  
20 3.23 5.63 2.84 4.24 4.24  
25 2.45 2.84 3.70 3.34 3.15  
30 6.67 0.34 2.45 1.75 1.70  
35 2.45 0.34 3.14 1.84 1.19  
40 8.73 3.53 4.73 4.73 4.08  
45 4.51 11.53 8.92 8.92 8.27  

Figure 9. Table of improved algorithm perimeter values for nine rotated squares, at five different resolutions

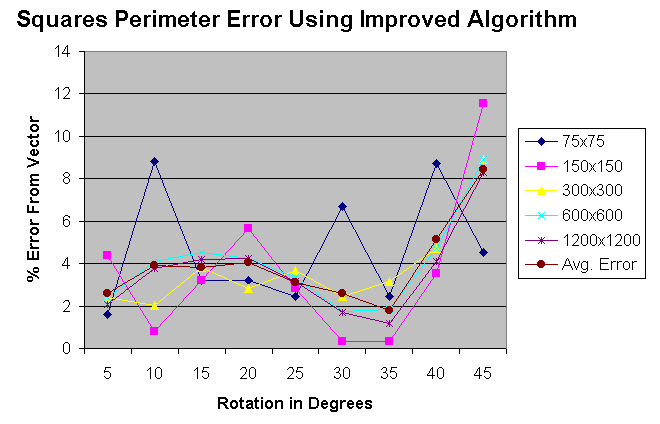
Figure 10. Chart of improved algorithm perimeter error for nine rotated squares, at five different resolutions

6.2 Perimeter Test 2.

A vector map of China was selected due to the variety of polygon shapes and sizes within its boundaries. The map, containing 29 polygonal regions, was rasterized in IDRISI, at 5 different resolutions (80x70, 160x140, 320x280, 640x560 and 1280x1120 pixels for an image 320x280 units, or 4,2,1,0.5,0.25 units/pixel respectively), and the perimeter and area of each rasterized polygon was computed and compared to its vector equivalent. This was done to show the effect that resolution had on the perimeter/area calculation results from IDRISI. The improved algorithm was also used to calculate the perimeters and areas of the polygons. Figure 11 shows an example of the vector map superimposed on the rasterized version, at the selected resolution. The aliasing is evident on most of the polygon boundaries. The results of the IDRISI perimeter calculation, including average error from the exact vector values, are shown in Figure 12. As can be seen, errors of up to 28% can result from area boundaries containing severe aliasing. Figure 13 graphically shows, at each resolution, the perimeter error for each polygon using the IDRISI perimeter calculation. Error typically gets worse, ranging from an average of 8.5% to 25.7%, as resolution increases, due to increased aliasing. The results of the improved algorithm perimeter calculation, including average error from the exact vector values, are shown in Figure 14. Figure 15 graphically shows the error of the perimeter calculation, at 5 different resolutions, using the improved algorithm. In this case, error improves, ranging from an average of 15.9% to 1.3%, as resolution increases. This can be attributed to the diagonal compensation properties of the improved algorithm, which has a better performance as resolution increases. At higher resolutions, there are smaller sized, but more aliased or diagonal sections on raster polygonal boundaries. Thus, at the highest resolution, 1280x1120 pixels for an image that is 320x280 in vector space (0.25 units/pixel), the average error reduces from about 25.7% to about 1.3%

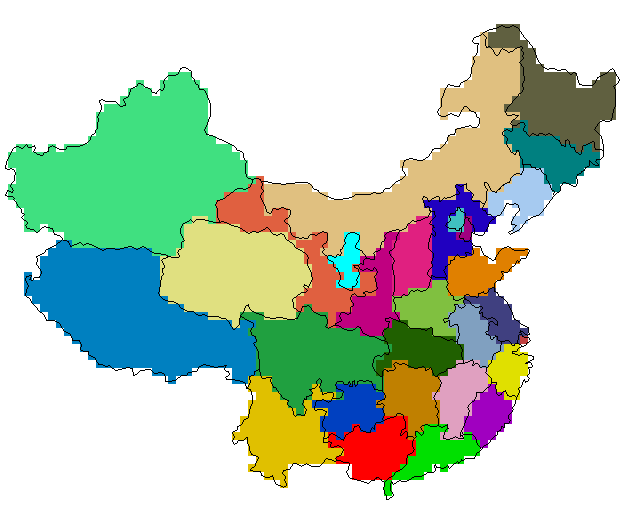
Figure 11. Test 2 – Rasterized map of China with vector boundary overlay (80x70 pixels)
  Resolution - Perimeter Values using IDRISI          
Polygon 80x70 160x140 320x280 640x560 1280x1120 Vector
1 488 512 536 542 544.5 432.69
2 416 456 478 472 481 384.48
3 304 320 340 345 349.5 281.37
4 176 200 204 207 210 164.88
5 160 164 172 186 190 151.79
6 320 348 354 368 374 299.86
7 272 296 310 314 318 251.04
8 400 420 436 441 442.5 346.61
9 104 112 114 112 115 90.05
10 192 228 244 249 248 200.02
11 168 180 182 195 193 154.50
12 152 176 182 197 194.5 155.62
13 192 208 216 218 221.5 175.54
14 112 124 128 134 135.5 107.09
15 144 156 162 164 165 129.12
16 96 124 130 139 140 111.21
17 16 20 24 24 25 19.36
18 120 132 164 163 163 128.85
19 120 144 174 177 175.5 142.61
20 144 156 166 173 176 139.42
21 136 160 170 176 177.5 142.00
22 120 152 158 160 163 128.97
23 216 248 270 285 287.5 228.51
24 40 40 38 39 41 33.34
25 152 184 184 192 190.5 152.57
26 176 208 220 229 228 179.42
27 312 344 368 376 375 293.66
28 664 748 762 763 776 618.06
29 40 40 42 44 44 36.32
             
  Resolution - %Error using IDRISI          
Polygon 80x70 160x140 320x280 640x560 1280x1120  
1 12.78 18.33 23.88 25.26 25.84  
2 8.20 18.60 24.32 22.76 25.10  
3 8.04 13.73 20.84 22.61 24.21  
4 6.75 21.30 23.73 25.55 27.37  
5 5.41 8.04 13.31 22.54 25.17  
6 6.72 16.05 18.06 22.72 24.73  
7 8.35 17.91 23.49 25.08 26.67  
8 15.40 21.17 25.79 27.23 27.66  
9 15.50 24.38 26.60 24.38 27.71  
10 4.01 13.99 21.99 24.49 23.99  
11 8.74 16.50 17.80 26.21 24.92  
12 2.33 13.10 16.95 26.59 24.98  
13 9.38 18.49 23.05 24.19 26.18  
14 4.59 15.79 19.53 25.13 26.53  
15 11.53 20.82 25.47 27.02 27.79  
16 13.68 11.50 16.90 24.99 25.89  
17 17.37 3.28 23.94 23.94 29.10  
18 6.87 2.44 27.28 26.50 26.50  
19 15.86 0.97 22.01 24.11 23.06  
20 3.28 11.89 19.06 24.08 26.23  
21 4.22 12.68 19.72 23.95 25.00  
22 6.95 17.86 22.51 24.06 26.39  
23 5.48 8.53 18.16 24.72 25.81  
24 19.99 19.99 13.99 16.99 22.99  
25 0.37 20.60 20.60 25.84 24.86  
26 1.91 15.93 22.61 27.63 27.07  
27 6.25 17.14 25.32 28.04 27.70  
28 7.43 21.02 23.29 23.45 25.55  
29 10.12 10.12 15.63 21.13 21.13  
  8.53 14.90 21.23 24.52 25.73 Average % Error
             

Figure 12. Table of IDRISI perimeter values for the 29 polygons of China, at five different resolutions

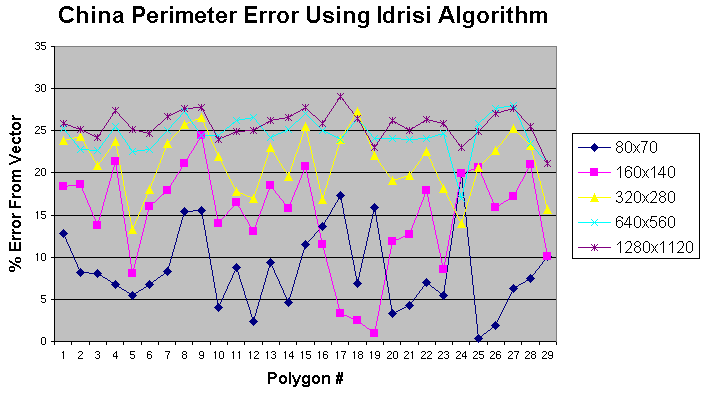
Figure 13. Chart of IDRISI perimeter error for the 29 polygons of China, at five different resolutions
  Resolution - Perimeter Values using Improved Algorithm          
Polygon # 80x70 160x140 320x280 640x560 1280x1120 Vector
1 386.89 424.65 443.69 439.80 439.23 432.69
2 329.03 386.67 395.25 387.99 389.19 384.48
3 234.49 266.31 280.76 283.11 285.22 281.37
4 140.56 156.69 162.12 166.21 168.20 164.88
5 132.26 144.09 143.87 156.61 155.28 151.79
6 274.80 292.45 293.52 304.43 304.80 299.86
7 221.68 247.10 250.25 252.27 253.18 251.04
8 350.58 346.93 354.56 355.68 351.89 346.61
9 83.23 92.20 95.31 91.65 90.98 90.05
10 173.34 191.96 202.35 205.70 200.89 200.02
11 119.27 150.75 150.21 158.62 155.97 154.50
12 119.36 153.74 151.93 161.77 157.78 155.62
13 161.47 169.77 172.48 177.73 176.64 175.54
14 82.67 105.14 105.63 106.66 107.54 107.09
15 111.36 126.75 129.73 131.94 130.62 129.12
16 70.84 107.94 109.86 111.48 111.96 111.21
17 16.00 15.20 18.94 18.67 19.89 19.36
18 100.26 104.24 132.14 130.82 129.77 128.85
19 99.06 117.36 140.60 142.00 142.93 142.61
20 119.74 118.45 133.38 136.95 140.05 139.42
21 104.04 139.74 142.40 144.23 143.66 142.00
22 106.02 128.69 131.45 129.60 130.56 128.97
23 183.36 196.47 228.40 232.94 230.81 228.51
24 33.20 37.46 32.41 34.29 34.28 33.34
25 122.84 148.71 147.05 147.15 147.08 152.57
26 146.67 163.57 177.99 183.49 181.89 179.42
27 270.97 285.77 301.61 296.86 297.08 293.66
28 542.97 618.81 624.26 621.18 623.94 618.06
29 30.41 33.72 35.01 38.67 36.97 36.32
             
  Resolution - %Error using Improved Algorithm          
Polygon # 80x70 160x140 320x280 640x560 1280x1120  
1 10.58 1.86 2.54 1.64 1.51  
2 14.42 0.57 2.80 0.91 1.22  
3 16.66 5.35 0.22 0.62 1.37  
4 14.75 4.96 1.67 0.81 2.02  
5 12.86 5.07 5.22 3.18 2.30  
6 8.36 2.47 2.11 1.53 1.65  
7 11.70 1.57 0.32 0.49 0.85  
8 1.15 0.09 2.29 2.62 1.52  
9 7.57 2.39 5.85 1.78 1.03  
10 13.34 4.03 1.16 2.84 0.44  
11 22.80 2.42 2.78 2.67 0.95  
12 23.30 1.21 2.37 3.95 1.39  
13 8.02 3.29 1.74 1.25 0.63  
14 22.80 1.82 1.36 0.40 0.42  
15 13.76 1.83 0.48 2.19 1.17  
16 36.30 2.94 1.21 0.25 0.67  
17 17.37 21.48 2.21 3.57 2.71  
18 22.19 19.11 2.55 1.52 0.71  
19 30.54 17.71 1.41 0.43 0.22  
20 14.12 15.04 4.34 1.78 0.45  
21 26.73 1.59 0.28 1.57 1.17  
22 17.79 0.21 1.93 0.49 1.23  
23 19.76 14.02 0.05 1.94 1.00  
24 0.40 12.38 2.79 2.84 2.84  
25 19.49 2.53 3.62 3.55 3.60  
26 18.25 8.84 0.80 2.27 1.37  
27 7.73 2.69 2.71 1.09 1.17  
28 12.15 0.12 1.00 0.50 0.95  
29 16.29 7.16 3.62 6.46 1.77  
  15.90 5.68 2.12 1.90 1.32 Average % Error

Figure 14. Table of improved algorithm perimeter values for the 29 polygons of China, at five different resolutions

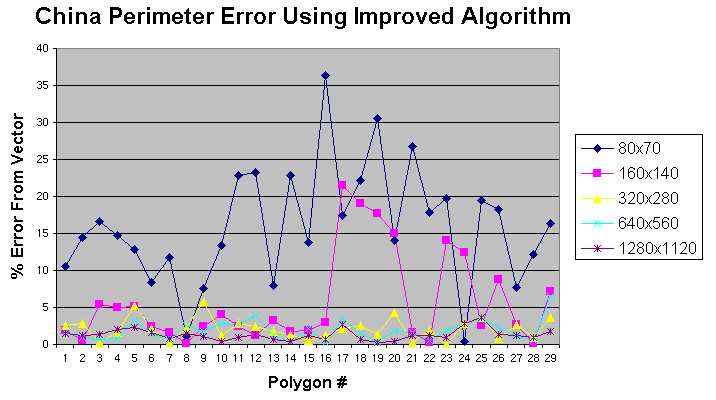
Figure 15. Chart of improved algorithm perimeter error for the 29 polygons of China, at five different resolutions

7. Area Test

It was originally thought, when this research began, that corrections for aliasing would improve the perimeter and area calculations in raster GIS. We have confirmed that this is true for the perimeter calculation, but little improvement can be made to the results of the area calculation. Errors in the area calculation are a result of the rasterization process, and the raster representation of a vector boundary. Upon examining Figure 11, one can see that the vector boundary includes parts of pixels and excludes parts of other pixels. In raster space, this ‘extra’ area and ‘excluded’ area, along the perimeters, cancel each other out. At higher resolutions, these extra and excluded areas are much smaller, since pixel size is smaller, and so this ‘cancelling out’ process is more precise. Figure 16 and Figure 17 show the error of the area calculations for the 9 squares and China map using IDRISI. As can be seen, errors are typically much less than 1% at the higher resolutions.

 
  Resolution - % Error using IDRISI Area Calculation          
Rotation in Degrees 75x75 150x150 300x300 600x600 1200x1200  
5 0.48 0.16 0.00 0.04 0.01  
10 0.48 0.80 0.00 0.12 0.03  
15 0.48 0.16 0.00 0.04 0.00  
20 0.48 0.16 0.32 0.08 0.00  
25 0.48 0.80 0.16 0.04 0.00  
30 0.48 0.16 0.00 0.00 0.00  
35 0.48 0.48 0.16 0.12 0.05  
40 0.48 0.48 0.16 0.00 0.00  
45 7.20 2.08 0.80 0.60 0.11  
  1.23 0.59 0.18 0.12 0.02 Average % Error

Figure 16. Area calculation for the nine squares using IDRISI

 
  Resolution - % Error using IDRISI Area Calculation          
Polygon 80x70 160x140 320x280 640x560 1280x1120  
1 0.669152 0.011575 0.048205 0.025788 0.011777  
2 0.615977 0.651676 0.18687 0.003278 0.002004  
3 1.845 0.675916 0.297778 0.203244 0.00158  
4 2.22726 0.911296 0.35084 0.013457 0.035583  
5 3.285293 1.550443 0.794859 0.225179 0.124279  
6 3.036828 0.091075 0.27507 0.161917 0.009546  
7 2.214409 0.563156 0.165955 0.077082 0.003207  
8 3.22389 1.175024 0.612035 0.161211 0.019213  
9 0.115682 1.353205 0.985983 0.023876 0.022026  
10 1.272667 0.343386 0.074044 0.242383 0.124546  
11 1.887871 3.330859 0.322252 0.003918 0.052844  
12 2.210303 1.87811 0.166096 0.089429 0.006393  
13 2.151617 0.234929 0.533247 0.175258 0.063389  
14 5.630619 0.877615 0.139297 0.064085 0.050317  
15 3.278122 0.204369 0.256694 0.012259 0.012259  
16 1.590532 0.377657 0.606438 0.254645 0.162386  
17 28.13839 10.17298 7.792422 1.19028 0.067442  
18 7.197181 2.043471 0.533385 0.082435 0.030303  
19 2.384302 1.597078 0.219437 0.071833 0.096434  
20 0.119253 1.399775 0.200878 0.080829 0.0108  
21 4.849846 1.410033 0.311434 0.040684 0.070028  
22 1.250159 1.836736 0.94147 0.246918 0.052125  
23 4.353677 2.167663 0.006117 0.074048 0.0231  
24 18.8817 4.021485 1.551094 1.086712 0.538623  
25 8.195964 0.328696 0.820504 0.492632 0.000825  
26 2.96541 0.123552 0.262568 0.187906 0.029287  
27 1.057194 0.196822 0.233364 0.008616 0.035502  
28 0.326883 0.417495 0.012912 0.04372 0.021407  
29 14.27761 2.864031 1.435561 1.421379 0.082188  
  4.456993 1.476211 0.694373 0.233276 0.060669 Average % Error

Figure 17. Area calculation for the China map using IDRISI

Empirical evidence shows that, as the resolution becomes coarser, the perimeter results improve, while the area results degrade. As the resolution becomes finer, the perimeter results degrade while the area results improve. This can be attributed to, at finer resolutions, the greater number of smaller aliased pixels on diagonal edges.

8. Conclusions

The preceding research has verified that several GIS packages use simplistic methods to calculate perimeters and areas of raster regions. For perimeter, these systems count the number of pixel edges that make up the perimeter of a raster region, multiplied by the length of the side of a pixel. For area, they count the number of pixels contained in a raster region, multiplied by the area of a pixel. The results for perimeter can be in error by as much as 40%. The algorithm presented here compensates for the aliasing, and shows significant improvement in the perimeter results, by an order of magnitude. For area calculations, it was determined that no significant improvement could be made to the existing method used in most GIS systems.

It must be noted that scale of the maps was never mentioned. The shape of the polygon, the scale of the map, and the size of the pixel (or the image resolution) all affect the results of the perimeter calculation. The boundary of a geographic region exhibits a fractal like behaviour, and the resolution of the image plays an important role in the ability to resolve the complex shape of a typical vector boundary in raster space. If resolution is poor, then significant features of reality are not represented properly, and so results from the perimeter calculation degrade, regardless of the method. It was thought that scale was not an issue, since the algorithm was improving upon the ‘measuring stick’ used to calculate the perimeter, regardless of scale. For classified remotely sensed imagery, where no real ‘vector boundary’ exists since the image is acquired in its native raster format, this algorithm can provide better perimeter results by approximating the apparent vector boundaries imbedded within the image.

Future work, to improve the performance of the algorithm, can include the resolution issue, possibly using fractal techniques, and adjustments to the perimeter values associated with each 3x3 pixel matrix.

Acknowledgements

I would like to thank Dr. Doug King and Evan Seed for their valuable insight and discussions pertaining to the implementation of the algorithm. I am also indebted to Danny Patterson, Jason Fournier, Casey Trull, Hassan Eljaji, and Bruce Thomas for their assistance in performing the perimeter and area experiment using the other GIS packages. Thanks to Klaus Carter for his invaluable help in formatting this document into HTML.

References

Clarke, Keith, "Analytical and Computer Cartography", Englewood Cliffs, N.J.: Prentice-Hall, Inc., 1995

Monmonier, Mark S., "Computer Assisted Cartography – Principles and Prospects", Englewood Cliffs, N.J.: Prentice-Hall, Inc., 1982

Cromley, Robert G., "Digital Cartography", Englewood Cliffs, N.J.: Prentice-Hall, Inc., 1992