Return to GeoComputation 99 Index

Principles of semantic modeling of landform structures

Martin Dehn, Holger Gärtner, and Richard Dikau
Geographisches Institut, Universität Bonn, Meckenheimer Allee 166, D-53115 Bonn Germany
E-mail: martin@giub.uni-bonn.de

Abstract

Landform as a result of various processes acting on the surface has also the function of a static boundary condition for processes in geomorphology, hydrology, meteorology, and others. The description, parameterization, and modeling of landform structures, as well as the definitions of nomenclatures, are fitted to the requirements of the mentioned disciplines and are therefore often strongly divergent. As a consequence, representations of landform structures of different disciplines often are not compatible and require frequent revisions and adaptations. Within an interdisciplinary Postgraduate School at the University of Bonn, geoscientific disciplines are working together with mathematics, photogrammetry and computer science in order to derive a comprehensive insight into some of the problems. Principles of the semantic approach will be presented in this paper. The main objective is a semantically correct description of landform which is useful to all disciplines related to surface structure. The presented approach is focusing on geometric form as a basic property extended by topological considerations and semantic definitions. The latter is an actual field of research. The potential, limitations and open questions of the semantic based approach, are discussed for the term hillslopes as a case study. The focus of the paper is on semantic representation in the first place, and only thereafter, special features of DEMs, tools, and implementations have to be considered.

1. Introduction

Landform is a central research object of geomorphology. As a subdiscipline (geo)morphometry is dealing with the qualitative and quantitative description and measurement of landform. We use landform structure in the title taking into account that landform is not essentially chaotic but structured due to a long history of geologic and geomorphic processes generating the presently visible landform. The definition and extraction of landform structures is of importance for other fields of science that treat landform as a boundary condition for their models. This topic is the central objective of an interdisciplinary Postgraduate School (Graduiertenkolleg) on landform structure that was established at the University of Bonn in 1998. The presented study is carried out in the frame of this Postgraduate School.

Mathematically, landform is a continuous surface covering the earth. All major approaches representing landform treat this surface as composed of smaller units. Operations that usually are carried out on the landform, or parts of it, are filter functions, delimitation of specific units following different sets of definitions and aggregation to larger forms or objects. The former two heavily depend on geometrical properties and methods. Nowadays all approaches are computer-based and rely on digital elevation models (DEM) of various scales, sources, and kinds. Since computer-power and a large amount of digital elevation data became easily accessible, much more work is done in geomorphometry and neighboring fields (Pike, 1995) often with Geographical Information Systems (GIS) as tools.

Due to this increasing number of applications and research directions based on DEMs, there arise problems of very heterogeneous views, definitions and applications of landform, landform structures and landform components. One difference obviously is that for geomorphologists, landform possesses at least 2 important properties: it is (i) a result of past geomorphic and geologic processes, and (ii) landform is a controlling boundary condition for actual (geomorphic) processes. For other disciplines, dealing with landform is usually only the boundary condition--property that is of importance to their field. Depending on the processes that are discussed, landform is seen and modeled quite differently. Further, there exists a problem in the exchange of information and data about landform structures between people with different contexts in the background. This is one small example of the more general problem of interoperability, e.g., discussed for GIS (Vckovski, 1998).

Like the discussions on interoperability in GIS show, a solution can be expected from the use of a semantic model that links conceptual frameworks and the computer-based modeling of DEMs. After presenting general ideas we focus on the example hillslope that is a highly important element of landform and subject to several disciplines dealing with DEMs.

This paper is focusing on principles of semantic modeling of landform structures in order to facilitate an interdisciplinary exchange of ideas and concepts. The paper is organized as follows. After presenting classical approaches of landform representation with examples, we explain basic principles of semantic modeling. Then we fill the theoretical skeleton with examples of landform in general and go into detail with the case study hillslopes. After discussing the results, we close with conclusions.

It is noted that the authors are geomorphologists; therefore, the discussion is biased towards this discipline.

2. Classical approaches of landform representation

An overview about state-of-the-art in geomorphometry and related fields can be found in Pike (1995). Classification of landform types, extraction of landform components and modeling of landform associations are objectives of a series of research papers and projects in geography/geomorphology. Classification can be carried out, e.g., with descriptive statistics of parameters calculated from DEMs (Evans, 1972 O`Neill and Mark, 1987). Landform units may be extracted by delimiting homogeneous areas. Dikau (1989) for example proposed form facets (units with homogeneous gradient, aspect and curvature) and form elements (units with homogeneous plan and profile curvature) as basic components of landform. The extraction of ridge and channel patterns and subsequent catchment delimitation can be solved with pattern recognition, geometrical and topological approaches (e.g. Brändli, 1997). Sometimes it is only a simple combination of geometric landform derivatives that are of importance for a question. A famous example is the index ln (a / tan ß), with a the specific catchment area of a location (and its slope, which is a parameter for soil water content in various hydrological approaches (Quinn et al., 1997). Schmidt et al. (1998) and Florinsky (1998) provide exhaustive lists of variables and parameters that are commonly used for different purposes. None of the mentioned examples is applying semantic modeling explicitly in the approach.

3. Semantic modeling and landform representation

Within the geosciences, as in other disciplines, specified objects and their interrelations have to be seen as a mental model, simplifying real world conditions. According to Bishr (1998) these mental models are part of the "discipline perception world," which means that semantics are strongly dependent on the scientific discipline itself.

The term semantic modeling, or semantics, in the face of computer models can be defined as the conventions and definitions that closely capture the meaning of the user's ideas (Rishe, 1992). In an alternative formulation of Bishr (1998), semantics can be defined as relationships between computer representations and the corresponding real world feature within a certain context. So it depends on the user's meaning which part of the real world is important to be represented in the (computer) model. User's meaning is what was already introduced as discipline perception world above.

Geographic objects are mostly described in two ways, (i) based on geometry as mentioned in Section 2 and/or (ii) based on their semantics. The latter means that objects are named by scientists with specific backgrounds and contexts. Taking into account that everybody is using terms differently, especially if they are additionally transformed to a foreign language, it is clear that we end up with a heterogeneity of names. This can result in different terms for the same object or identical terms for different objects. But this naming heterogeneity is only part of the problem. The specific discipline perception worlds also cause a cognitive semantic heterogeneity that is situated deeper in the perception of reality and is more difficult to solve. An agreement on basic definitions of objects is necessary for their successful semantic representation.

In order to bring down these theoretical considerations to practical applications we describe some of the approaches of landform representation given in Section 2, especially focusing on semantic heterogeneity. Related to this, we indicate differences in the mental models of landform of these particular examples. In Table 1, a selection of landform derivatives is listed together with descriptors and objectives in order to exemplify that the purpose of a study also influences the way in which the real world landform is perceived. If we would ask members of the mentioned disciplines about the meaning or information content of an identical landform sector their answers will differ. This might be true also given the case that the same geometric descriptors were used. In order to overcome this perception and language barrier, we propose to formulate semantics of landform, landform structures and specific landform features. This is not only necessary for the implementation of interoperable GIS (see Bishr, 1998), but also to facilitate the interdisciplinary exchange of ideas between people working with DEMs.

Table 1. Selection of DEM-derivatives that are commonly used for landform representation,
classified because of various properties.

a) a is the specific catchment area of a location and ß its gradient

4. Case study hillslope

We take the term hillslope as an example because it is a central object in geomorphology and hydrology as well as other fields. According to Schumm and Mosley (1973) we have the situation of an "amazing absence of any precise definition of slope." On the other hand, hillslopes are an important part of geomorphology. Twidale (1960) saw hillslopes as the fundamental unit of the physiographic landscape. For Finlayson and Statham (1980) they are the basic elements of all landscapes. Hillslopes have a high geometrical importance in terms of characterizing various landscapes or landscape types (Chorley, 1964). All cited passages talk about hillslopes with an implicit concept of what it is, but like the first citation told, there is no precise definition even within geomorphology. By describing the form of a slope, Summerfield (1991) stated that "slope forms vary enormously, but in many cases they comprise an upslope convexity leading down to a rectilinear main slope, which terminates in a basal concavity. The main slope can consist of either a single segment or a more complex sequence of segments at different angles. . .." This statement is very near to the basic definitions developed in the next section, nevertheless, it is based on the cognitive world of geomorphology.

Further, there were already examples of naming heterogeneity visible because some people use slope, others hillslope, for naming the same object. We use the term hillslope in this paper. With these statements the importance of hillslopes is demonstrated. Further, none of the many books on hillslopes (e.g., Anderson and Brooks, 1996; Brunsden, 1971; Carson and Kirkby, 1972; Selby, 1993) provides a basic definition of the term; therefore, we present a set of definitions and hope to initiate a fruitful discussion on the topic.

4.1 Basic definitions

Starting with the most basic properties, the definition subsequently becomes more complex by the inclusion of more descriptors and specific contexts. The basic definitions are formulated independent of scale. On the other hand, it is clear that the term hillslope belongs to a certain scale in the discipline perception world. We refer to this issue later.

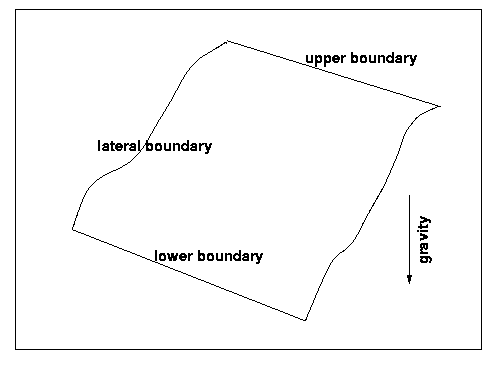
Figure 1. Typical scheme of a hillslope.

(1a) Hillslope is an inclined landform unit that is limited by at least two other units. A hillslope is a transition between an upper and a lower unit (Figure 1). So far we stressed a geometrical descriptor (gradient) and a topological descriptor (neighborhood/boundary). If we would apply this definition to a global DEM, nearly everything would be classified as hillslope that certainly is not in agreement with the perception of most geomorphologists; therefore we need restrictions to this most basic definition. It is true that all hillslopes have a gradient, but the inverse is not valid. Not all parts of landform with a gradient are called hillslope. (1b) The gradient of hillslopes is between an upper ß_max and lower ß_min threshold delimiting vertical walls like rock and mountain faces and plains, respectively, from hillslopes. We do not include overhang (negative gradient) in the discussion because they are difficult to represent in common DEMs, and they appear to be nearly unimportant concerning areal extent. (1c) The next geometric requirement for defining one hillslope is that no part of the specific unit has an elevation > upper boundary or an elevation < lower boundary of respective unit. This is not yet enough, a further restriction is (1d) the requirement of a minimum areal extent. The unit fulfilling all definitions so far--dependent on the scale of the investigation--should have a distinct size in direction of maximum gradient to delimit it from an edge or one side of a crest. If the classification is based on raster data, one also could argue that 1 or 2 or n raster cells are not sufficient to determine a hillslope. (The authors refer to the matter of size and scale later.)

This first set of definitions was based mainly on geometrical and topological considerations. The authors include statements that are more closely related to perceptions of the phenomenon, according to Bishr (1998) that are the cognitive heterogeneity of semantics. For the different disciplines, thematic descriptors appear to be important. Hillslopes may be perceived as areas where specific processes take place. This could be soil erosion by water, overland flow, landslides, and others. For a tourist manager, on the other hand, hillslopes could be areas where skiing is possible. In all these cases it is the sine of the slope angle as part of the gravitational force that is enables the actions. (2) We generalize that hillslopes are units where mass*gravitational force*sin (plays a dominant role for processes.

A part of the semantic heterogeneity arises from the fact that landform as a continuous surface is artificially delimited into units. Conceptions of landform features are often soft and features are not defined disjoint. Take mountains, hillslopes, and valleys as an example: they are certainly not the same and they are ordered in a toposequence, but how can that be defined where the valley is ending and the mountain is beginning? And where exactly is the transitional unit hillslope located? Landform concepts show many such cases of indeterminate boundaries (see Burrough and Frank, 1996 for related problems) and definitions then are quite strongly dependent on the discipline perception. (3) It is noted that various landform features cannot be defined with their internal properties alone. Definitions have to incorporate neighboring landform units. A valley, for example, is impossible to exist without its accompanying hillslopes. And no mountain can be constructed without the hillslopes surrounding it. In a formular way of description we have many intersecting categories in the definition of landform.

We already introduced the requirement of a minimum spatial extent for landform units to be classified as hillslope. But what about units that fulfill several requirements, but are very large in spatial extent? In this case it seems as if gradient becomes less important in comparison to horizontal extent of the unit. An example are plateaus or plains. They are not of 0 deg. gradient but, in comparison to their size, the sloping property is marginal. In a more complex case the altiplano of the Andes would not be perceived as hillslope due to the size effect and due to the neighboring mountain chains with steeper gradients. This highlights the importance of context in the way landforms are perceived and how definitions have to be formulated. Size as absolute property also can be an argument in the application of landform terms. If we take a 1m X 1m DEM with horizontal resolution of 1mm and extract a unit of 6cm X 8cm fulfilling the hillslope definitions above, most people would not agree to have a hillslope, we assume mostly because typical processes do not operate on this scale. (4) Size and scale context are important elements of definitions based on semantics. This is due to naming and cognitive heterogeneity.

(5) Examples of naming heterogeneity in the case of hillslopes are: hillslope, slope, valley-side, mountain flank, and finally, terms of other languages. In Table 2 we summarize the set of definitions for the term hillslope concerning the properties that were used. This provides an overview about the main properties of interest. The description is completed by indicating in which type of definitions discipline perception becomes important. A missing x is not signifying that it is not at all considered. For example, in the case of basic definitions, perception is without an x because the focus is on geometry and topology; however, as mentioned before, specific perception is present in all parts of definitions to a certain degree.

Table 2. Summary of the definitions suggested that for the term hillslope concerning main properties that were stressed, (x) completed with indications of cases in which discipline perception is important. Numbers in brackets refer to the respective number in the text.

4.2 Formalising the hillslope concept

After the presentation of verbal definitions of hillslope we are now going to formalise the concept. We describe a user sending a query in order to receive specific information about hillslopes. This user is doing this with his/her own cognitive model in mind. In our opinion it is necessary to firstly address a thesaurus representing synonyms of the query term (e.g., hillslope) and their relations to other disciplines in which they are used. This thesaurus has to be based on definitions typically used by all disciplines whose objectives are related to landform in any way. It has to be defined by participants of all related disciplines to guarantee a precise definition of the used terms. With this output, the user is able to (a) select specific synonyms for further queries or (b) by default to query on all synonyms. The next step is to get detailed information about cognitive worlds associated with the synonyms. This is represented by the frame "discipline perception" in Figure 2. This frame represents a data collection that is related to the thesaurus. The important difference has to be seen in the fact that information within this data collection is ordered by specific disciplines and extends the pure definition of the term stored in the thesaurus. It comprises detailed data about the usage of the identified term (or synonym) based on the research objectives of the discipline. This means that it describes the semantics (other than linguistic) and the syntax used in different disciplines to express the term and its relation to other real world objects. Knowledge about the syntax enables the user to analyze (i) the naming of semantics and to further reselect synonyms according to his objective and/or (ii) the geometric representation of the queried term. An overview concerning the procedure is depicted in Figure 2.

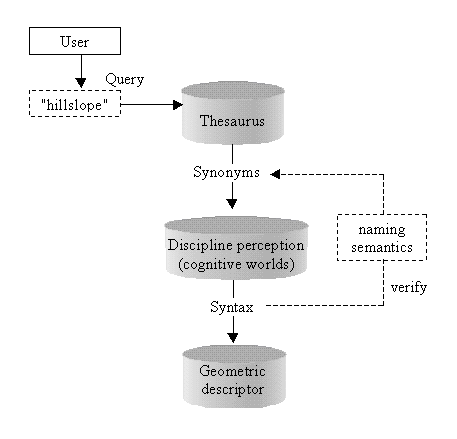
Figure 2. Conceptual overview of the semantic modeling approach represented by a query on the term hillslope.

5. Conclusions

We presented reasons for a semantically based approach to landform representation that goes beyond geometrical and topological considerations. One of the reasons to develop such an approach is to bring together perceptions, concepts, and definitions as belonging to different disciplines. This is a basic prerequisite in order (i) to clarify what (object) we are talking about, (ii) to enable the exchange of ideas between disciplines and (iii) to enable exchange of data sets. We based our approach on a concept proposed by Bishr (1998) in the face of interoperability in GIS, and adapted it to landform modeling with some details about the term hillslope.

The presented approach is still preliminary and is missing many aspects of landform structure and hillslopes. Respecting the fact that this theoretical approach is used as a base for the ongoing work, the next step will concentrate on the development and design of the thesaurus and the related data collection that represents the discipline perception worlds. This has to be done under consideration of the various standards on defining objects in geosciences and other disciplines. The design of this central part will be done using the Unified Modeling Language (UML) to represent all possible interrelations between semantic expressions and mathematically correct definitions of objects in different disciplines.

Future work will include semantic representations of further landform features, and the development of a scheme combining sets of semantic definitions and applications of the concept with DEMs of various landscape types and scales in order to test the validity of the assumptions.

Acknowledgments

This paper is part of the Graduiertenkolleg GRK-437/1 "Das Relief - eine strukturierte und veränderliche Grenzfläche" at the Universität Bonn, funded by the DFG and the land Nordrhein-Westfalen and the DFG-project "Open Palaeoecological Information System" (OPALIS).

References

Anderson, M.G. and S.M. Brooks, Eds., 1996. Advances in hillslope processes. Wiley, Chichester, p.1,306.

Bishr, Y., 1998. Overcoming the semantic and other barriers to GIS interoperability. Int. J. Geographical Information Science, 12 (4), pp. 299-314.

Brändli, M., 1997. Modelle und Algorithmen für die Extraktion geomorphologischer und hydrologischer Objekte aus digitalen Geländemodellen. Geoprocessing Reihe 32, Zürich, p. 176.

Brunsden, D., 1971. Slopes - form and process, Spec. Publ. 3. Inst. British Geographers, London, p. 175.

Burrough, P.A. and U.A. Frank, Eds., 1996. Geographic Objects with Indeterminate Boundaries. Gisdata, 2. Taylor & Francis, London, p. 345.

Carson, M.A. and M.J. Kirkby, Eds., 1972. Hillslope - form and process. Cambridge University Press, Cambridge, p. 475.

Chorley, R.J., 1964. The nodal position and anomalous character of slope studies in geomorphological research. Geol. J., 130, pp.70-73.

Dikau, R., 1989. The application of a digital relief model to landform analysis in geomorphology. In: J. Raper Ed., Three-dimensional applications in Geographical Information Systems. Taylor & Francis, London, pp. 51-77.

Evans, I.S., 1972. General geomorphometry, derivatives of altitude and descriptive statistics. In: R.J. Chorley Ed., Spatial analysis in geomorphology. Methuen, England, pp. 17-90.

Finlayson, B. and I. Statham, 1980. Hillslope analysis. Butterworth, England, p. 230.

Florinsky, I.V., 1998. Combined analysis of digital terrain models and remotely sensed data in landscape investigations. Progress in Physical Geography, 22 (1), pp. 33-60.

O'Neill, M.P. and D.M. Mark, 1987. On the Frequency Distribution of Land Slope. Earth Surface Processes and Landforms, 12, pp. 127-136.

Pike, R.J., 1995. Geomorphometry - progress, practice, and prospect. Z. Geomorph. Suppl.-Bd., 101, pp. 221-238.

Quinn, P.F., K.J. Beven and R. Lamb, 1997. The ln(a/tanß) Index: how to calculate it and how to use it within the TOPMODEL framework. In: K.J. Beven, Ed., Distributed hydrological modelling: applications of the TOPMODEL concept. Wiley, Chichester, England, pp. 31-52.

Rishe, N., 1992. Database design: the semantic modeling approach. McGraw-Hill, p. 528.

Schmidt, J., B. Merz and R. Dikau, 1998. Morphological structure and hydrological process modelling. Z. Geomorph. N.F., 112, pp. 55-66.

Schumm, S.A. and M.P. Mosley, Eds., 1973. Slope morphology. Benchmark Papers in Geology. Dowden, Hutchinson & Ross, Stroudsburg.

Selby, M.J., 1993. Hillslope Materials and Processes. Oxford University Press, Oxford, p. 451.

Summerfield, M.A., 1991. Global Geomorphology. An Introduction to the Study of Landforms. Addison Wesley Longman Limited, Harlow, p. 537.

Twidale, C.R., 1960. Some problems of slope development. J.Geol. Soc. Australia, 6, pp.131-147.

Vckovski, A., 1998. Special Issue: Interoperability in GIS. Int. J. Geographical Information Science, 12 (4), pp. 297-298.