Estimating a non-stationary spatial structure using simulated annealing

Olivier Perrin
INRA, Domaine Saint-Paul, Site Agroparc, 84914 Avignon Cedex 9 France
E-mail: perrin@avignon.inra.fr

Serge Iovleff
Laboratories SABRES, IUP Vannes-Tohannic, rue Yves Mainguy, 56000 Vannes France
E-mail: Serge.Iovleff@univ-ubs.fr

Abstract

In the last decade, a useful model for non-stationary random fields has been developed. This consists of reducing the random field of interest to isotropy via a bijective bi-continuous deformation of the index space. Then the problem consists of estimating this space deformation. We propose to estimate this space deformation using a constrained continuous version of the simulated annealing for a Metropolis dynamic.

1. Introduction

Assumption of isotropy is clearly violated for many, if not most, spatial environmental phenomena. Factors such as topography, local pollutant emissions, and meteorological influences may cause such assumptions to be violated. This has led to research into modelling spatially non-stationary second order structure, as reviewed in [7]. For dealing with this non-stationarity, Sampson and Guttorp [19] have developed a model that consists of reducing the correlation function r(x,y) of the spatial phenomenon of interest, modelled by a random field $% latex2html id marker 628$Z={Z(x), x in G subseteq mathbb {R}^{2}}$$ , to an isotropic one as follows

(1)

where denotes the Euclidean norm in $% latex2html id marker 632$mathbb {R}^{2}$$ , represents a bijective deformation of the geographic coordinate system and is an isotropic correlation function. In the sequel, we refer to the geographical coordinate system as the G-space $% latex2html id marker 640$subseteq mathbb {R}^{2}$$ , where G stands for geographical, and to the deformed coordinate representation as the D-space $% latex2html id marker 646$subseteq mathbb {R}^{2}$$ , where D stands for deformed.

Unlike the classical geostatistical models, non-stationarity through second order moments is thus taken into account and model (1) gives opportunity to enlarge the class of models for studying spatial environmental random fields.

When is strictly decreasing, Perrin and Meiring [16] prove the uniqueness of both the deformation and up to a homothetic Euclidean motion for and up to a scaling for . Perrin and Senoussi [18] give the general form of the deformation that reduces a non-stationary random field in the way (1), under smoothness assumptions.

Our concern in this paper is the estimation of the space deformation in model (1) when the isotropic correlation depends on a parameter $% latex2html id marker 664$beta in mathbb {R}^{q}$$ , . From now on, $rho_{beta}$ stands for the isotropic correlation function. This estimation is based on T repetitions (independent and identically distributed observations) of Z at each of n distinct monitoring sites $x_{1},x_{2},ldots,x_{n}$ in G, which may be irregularly located; we suppose that G represents the convex hull of these sites. We denote these records using Z_t(x_i), , .

So far, the deformation has mostly been estimated with the help of a non-parametric approach. This non-parametric estimation of has already been extensively developed, [11], [12] and [13], and applied in analyses of solar radiation [19], acid precipitation [8], rainfall [14], air pollution [3], tropospheric ozone [20], ...This approach consists of modelling using a pair of thin-plate splines and minimising a penalised weighted least squares criterion to estimate the D-space coordinates $Phi(x_{i})$ of the monitoring sites x_i, . This treatment is carried out with a Marquardt-type algorithm. At least, two drawbacks are associated with this method: (i) bijection condition is not ensured; (ii) the fitting of the model becomes a challenging numerical problem with dimensionality roughly proportional to the number of fixed monitoring sites [12].

Perrin and Monestiez [17] propose a parametric approach. They model using a composition of a "small'' number of bijective elementary radial basis deformations. Then they use a least squares criterion to estimate the parameters; this criterion is minimised in a classical way (Marquardt-type algorithm). Let us precise two disadvantages of this method: (i) so far there is no rational choice of the relevant number of elementary deformations; (ii) there is a considerable dependence on the starting values in the minimisation procedure.

To avoid all these disadvantages, we propose here to estimate in a first step the D-space coordinates $Phi(x_{i})$ , , by minimising an objective function with a stochastic algorithm, the continuous version of the simulated annealing for a Metropolis dynamic. To ensure a bijective correspondence between the n points in the G-space and their estimated deformations in the D-space, we impose some non-folding constraints in the algorithm. In a second step, to estimate the deformation in the whole G-space, we use a piecewise affine interpolation of the points x_i in the G-space and the estimations of their deformations $Phi(x_{i})$ in the D-space, .

The paper is structured as follows. In Section 2, we address the estimation problem of the deformation with the simulated annealing algorithm together with some non-folding constraints. In Section 3, we illustrate our non-parametric approach with precipitation data from 20 sites in the Languedoc-Roussillon region of France. Section 4 points out one possible application where the non-stationary model of a correlation function using space-deformation may be useful. More precisely, we give one idea of how spatial prediction should proceed in the new coordinate space and propose a cross validation study to demonstrate the possible improvement due to the deformation in predictions. Further, we apply this cross validation study to our precipitation data set. Finally, Section 5 discusses two extensions and future directions related to this work.

2. Estimating the space deformation using a constrained simulated annealing

2.1 Definition of the objective function

The repetitions of Z allows us to define the sample correlation estimates $hat{r}(x_{i},x_{j})$ for each couple of sites (x_i,x_j),

$begin{displaymath}hat{r}(x_{i},x_{j})=frac{displaystylesum_{t=1}^{T}(Z_{t... ...displaystylesum_{t=1}^{T}(Z_{t}(x_{j})-bar{Z}(x_{j}))^{2}}}end{displaymath}$

(2)

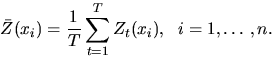where $bar{Z}(x_{i})$ are the sample mean estimates: $$bar{Z}(x_{i})=displaystylefrac{1}{T}displaystylesum_{t=1}^{T}Z_{t}(x_{i}),$ We denote using $y_{i}=Phi(x_{i})$ , , the positions of the sites in the D-space and we define $hat{y}_{1},hat{y}_{2},ldots,hat{y}_{n}$ and as the estimations of $y_{1},y_{2},ldots,y_{n}$ and which minimise the following objective function

$begin{displaymath}U(y^{star}_{1},y^{star}_{2},ldots,y^{star}_{n},beta^{s... ...j})-rho_{beta}(Vert y^{star}_{j}-y^{star}_{i}Vert)]^{2},end{displaymath}$

(3)

with respect to the parameters $y^{star}_{1},y^{star}_{2},ldots,y^{star}_{n}$ and $beta^{star}$ , and subject to some non-folding constraints described in Paragraph 2.2.

We know from Perrin and Senoussi [18] and Perrin and Meiring [16] that the bijective deformation and the isotropic correlation in (1) are unique up to a homothetic Euclidean motion for the deformation and up to a scaling for the correlation. The practical implication of this result is that we can fix two site positions in the minimisation procedure to fix translations, rotations and scalings.

2.2 Minimising the objective function using constrained simulated annealing

The objective function (3) is minimised using a continuous state version of the simulated annealing algorithm ([6], [10], [1], [5] and [2] for seminal references) subject to some non-folding constraints.

Among others, simulated annealing has the following advantages:

it explores the whole objective function's surface and tries to optimise the function while moving both uphill and downhill; thus, it is largely independent of the starting values, often a critical input in conventional algorithms;
it can escape from local minima and go on to find the global minimum by the uphill and downhill moves;
it makes less stringent regularity assumptions regarding the function than do conventional algorithms (it need not even be continuous).

For all these reasons and because of the high complexity of our objective function (3), we use simulated annealing for minimising (3). However, let us precise that in our particular context, the main advantage of this algorithm consists of its great flexibility. By this we mean that it can include non-folding constraints to ensure a bijective estimation of .

2.2.1 Definition of the objective function

We describe hereafter the different steps to minimise (3) with non-folding constraints
- step 0: we start from the geographical configuration of the sites (G-space). We set $y(0)={y_{i}(0)=x_{i}, i=1,2,ldots,n}$ . Then to give an initial value to $beta^{star}$ , minimise the objective function (3) with respect to $beta^{star}$ (y(0) is hold fixed) with a Marquard-type algorithm. Let be the estimation of at step 0. Finally, take a sequence of "temperatures'' $(c_{0},c_{1},ldots,c_{k},ldots)$ decreasing to 0 by steps of length n

$begin{displaymath}% latex2html id marker 792c_{k}=theta^{lfloor k/n rfloor}c_{0},$

- step k: let $y(k-1)={y_{i}(k-1), i=1,2,ldots,n}$ be the estimated position of the sites. The change proposition is: fix $beta^{star}=beta(k-1)$ , choose only one site (candidate point) j uniformly among the n sites and move it locally at a position y with natural non-folding constraints we precise hereafter. The other sites are hold fixed. Then:

if $Delta_{k} U = U(beta^{star},y,y_{i}(k), i neq j)-U(beta^{star},y_{i}(k-1)) leq 0$ then we take y_j(k)=y;
otherwise sample an uniform law V in [0,1]

if $% latex2html id marker 814$V leq exp(-Delta_{k}U/c_{k})$$ , take y_j(k)=y;
otherwise keep y_j(k)=y_j(k-1).

then we minimise (3) with respect to $beta^{star}$ (y(k) is hold fixed) and let be the estimation of at step k;
stopping criterion: if $U(beta(pn),y(pn))-U(beta((p+1)n),y((p+1)n))<10^{-8}$ for two consecutive values of the integer p we stop the algorithm.

2.2.2 Description of the non-folding constraints

These constraints account for global and local non-foldings.

First, we embed G in a rectangle . We precise the function of this rectangle further.

Second, we construct the Delaunay triangulation (cf. [15] for instance) for the n geographical sites plus the 4 vertices of as well as the 4 mid-points of its 4 edges. For computing the Delaunay triangulation we use a program written by Shewchuk [21].

For each site x_i, , we identify all the triangles for which this site is a vertex. Then consider the polygon composed with the aggregation of these triangles and denote using $A_{i,1},A_{i,2},ldots,A_{i,q_{i}}$ its vertices, where q_i is the number of triangles. We assume that these vertices are ordered clockwise and denote using (A¹_i,l,A²_i,l) their coordinates , $l=1,2,ldots,q_{i}$ .

At step k of our algorithm, a point y_j(k-1) is moved at a position y. To ensure non-folding constraints, in other words to avoid that triangles overlap, we impose that this new position is chosen uniformly in a convex polygon $mathcal{C}^{k}_{j}$ which is the set of points M_j=(M_j¹,M_j²) such that:

$begin{displaymath}M_{j}^{1}(A^{2}_{j,l}-A^{2}_{j,l+1})+M_{j}^{2}(A^{1}_{j,l+1}... ...-A^{1}_{j,l+1}A^{2}_{j,l} < 0,$

with the convention q_j+1=1. This inequality means that for any M_j in $mathcal{C}^{k}_{j}$ the segment [y_j(k-1),M_j] do not intersect any of the line (A_j,l,A_j,l+1). The region $mathcal{C}^{k}_{j}$ corresponds to the marked area of Figure 1

Figure 1: The marked area corresponds to the non-folding constraints.

begin{figure}% latex2html id marker 299centerline{epsfig {figure=contr.ps.eps, width=8cm}}end{figure}

These constraints mean that we impose moves in the simulated annealing algorithm that preserve the topological structure of the Delaunay triangulation the same before and after the deformation.

The rectangle allows us to write the previous constraints in a similar way for all the sites. Indeed, each site of G is included in a polygon for which the vertices are also vertices of the Delaunay triangulation for the n sites and the 8 points of . Without this embedding, we would have to distinguish between the boundary points of G (the vertices of the convex hull) and its interior points. Moreover, the embedding of G in prevents us from global folding of G in itself. In conclusion, we can say that the Delaunay triangulation accounts for local non-foldings and that the embedding of G in accounts for global non-foldings.

2.2.3 Estimating the deformation on the whole G-space

Any point x in G belongs to a (unique) triangle for which the vertices are three monitoring sites, say x_i, x_j and x_k. Thus, any point x is uniquely defined by its barycentric coordinates in the triangle ${x_{i},x_{j},x_{k}}$ as follows

x=a_x,ix_i+a_x,jx_j+a_x,kx_k

where $(a_{x,i},a_{x,j},a_{x,k})in [0,1]^{3}$ such that a_x,i+a_x,j+a_x,k=1. We define the estimation at point x of the deformation as follows

$begin{displaymath}hat{Phi}(x)=a_{x,i}hat{y}_{i}+a_{x,j}hat{y}_{j}+a_{x,k}hat{y}_{k}end{displaymath}$

where $hat{y}_{i}$ , $hat{y}_{j}$ and $hat{y}_{k}$ are estimated with the simulated annealing algorithm. So defined, the estimation holds the following features: continuous; bijective; an interpolant, i.e. $hat{y}_{i}=hat{Phi}(x_{i})$ , .

3. Application to a real data set

3.1 The data

They consist of monitored precipitation data from n=20 sites in the Languedoc-Roussillon, south of France, for which the geographical configuration is shown in Figure 2.

Figure 2: Site locations with department and coast contours at the top, and the corresponding Delaunay triangulation below.

begin{figure}% latex2html id marker 354epsfig {figure=leilei1.ps,width=8cm}epsfig {figure=fig2.ps,width=3cm}end{figure}

These data are in the form of 10-day aggregates, giving 6 records during November and December each year from 1975 through 1992 (T=108). These data hold the following features: (i) a low frequency of missing values; (ii) a similar altitude (between 0 and 200 meters) for all the sites so that an altitude correction is pointless; (iii) a homogeneous period in the year so that a seasonal adjustment is not necessary. As pointed out by Meiring [11], means and variances are positively related, and therefore, sample correlations between observations are calculated on the scale, after adding 1 to all observations.

The sample correlation estimates for a pair of sites is based on all the time points for which both sites has observations. The sample correlations for different pairs of sites are sometimes based on different numbers of observations, so that the sample correlations matrix is not positive definite; however, the model (1) fitted to the sample correlation remains positive definite.

3.2 Estimation of the model

3.2.1 Isotropic correlation function model

The upper right-hand plot in Figure 5 represents the geographical inter-site distances versus the corresponding correlations $hat{r}(x_{i},x_{j})$ 1<i<j<n defined by (2), to which one would fit an isotropic correlation model if we assume weak isotropy for Z (note this means that is the identity function in (1)). According to this plot, we decide to use the exponential model

$begin{displaymath}% latex2html id marker 972rho_{beta}(u)=expdisplaystyleleft(-beta uright),$

so that the objective function (3) is re-written as follows

$begin{displaymath}% latex2html id marker 378U(y^{star}_{1},y^{star}_{2},ld... ...beta^{star}Vert y^{star}_{j}-y^{star}_{i}Vertright)]^{2}.end{displaymath}$

(4)

3.2.2 Results and conclusions

For minimising (4) we apply our constrained procedure described in Paragraph 2.2. The Delaunay triangulation for the 20 sites is shown in Figure 2. In the cooling schedule we take c₀=1000 and . Figure 3 shows the estimated deformation of the Delaunay triangulation.

Figure 3: Deformation of the Delaunay triangulation.

begin{figure}% latex2html id marker 404centerline{epsfig {figure=simpleexp3.ps,width=3cm}}end{figure}

The estimated deformations of the G-space coordinates also are illustrated by Figures 4. In this figure, the motion from one site in the G-space to its estimated position in the D-space is represented by an arrow.

Figure 4: Plot of the estimated spatial deformation from the G-space (circles) to the D-space (black dots).

begin{figure}% latex2html id marker 412centerline{epsfig {figure=simpleexp2.ps, height=5cm}}end{figure}

The upper right-hand plot of Figure 5 shows the fitted exponential correlation as a function of the D-space coordinates. The G-space has been stretched in regions of relatively lower correlations, and shrunk in regions of relatively higher correlations, so that the exponential correlation better models the correlations in the D-space representation (minimum of the objective function is equal to 0.022) than in the G-space representation (minimum of the objective function is equal to 0.155). Improvement of this fitting is illustrated by the interquartile intervals: the empirical correlations are less scattered in the D-space than in the G-space.

Figure 5: At the top and on the left, inter-site distances in the G-space $Vert x_{j}-x_{i}Vert$ versus empirical correlations $hat{r}(x_{i},x_{j})$ and the fitted exponential correlation model (solid line). At the top and on the right, inter-site distances in the estimated D-space $Verthat{Phi}(x_{j})-hat{Phi}(x_{i})Vert$ versus empirical correlations $hat{r}(x_{i},x_{j})$ and the fitted exponential correlation model (solid line). At the bottom and on the left, box-plots of the empirical correlations as a function of the distances in the G-space. At the bottom and on the right, box-plots of the empirical correlations as a function of the distances in the D-space.

begin{figure}% latex2html id marker 418begin{center}includegraphics [height=8cm]{simpleexp1.ps}end{center}end{figure}

4. Applications of the space deformation model to the prediction

We point out one possible application where the space deformation model (1) may be useful. This is the prediction using Kriging. We refer to Cressie [4] for a presentation of the Kriging method.

In practice the mean and the variance fields are very seldom known, and must be predicted. As Høst et al., illustrate [9], separate modelling of the mean, variance and residual fields from monitoring data collected in space and time, may give very valuable information about the standard errors in spatial interpolation. Prediction of each of the mean, variance, and residual field contributes to the overall spatial interpolation errors; however, estimation of the mean and variance is not the topic of this work and we concentrate only on the prediction of the centred and standardised random field Z.

To predict the centred and standardised random process Z at any location we use the simple Kriging predictor

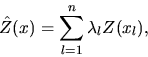
$begin{displaymath}hat{Z}(x)=displaystylesum_{l=1}^{n}lambda_{l}Z(x_{l}),end{displaymath}$

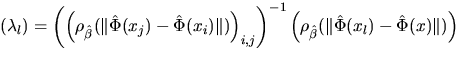with $(lambda_{l})=displaystyleleft(displaystyleleft(rho_{hat{beta}}(Verth... ...tyleleft(rho_{hat{beta}}(Verthat{Phi}(x_{l})-hat{Phi}(x)Vert)right)$ where $(lambda_{l})$ denote the vector of the Kriging coefficients, $displaystyleleft(rho_{hat{beta}}(Verthat{Phi}(x_{j})-hat{Phi}(x_{i})Vert)right)_{i,j}$ the correlation matrix of the vector $(Z(x_{1}),Z(x_{2}),ldots,Z(x_{n}))$ and $displaystyleleft(rho_{hat{beta}}(Verthat{Phi}(x_{l})-hat{Phi}(x)Vert)right)$ the correlation vector between the ``known sites'' $(Z(x_{1}),Z(x_{2}),ldots,Z(x_{n}))$ and the ``unknown site'' Z(x).

One way to check whether the deformation may improve the prediction is a cross validation study. More precisely, at each time t, we set aside a site and we predict the value of Z at this site with the n-1 remaining sites using the simple Kriging predictor described above. We repeat this operation for each of the n sites T times. Then we calculate the mean square error prediction that has to be compared with the one we would obtain using the fitted isotropic correlation function if we assume weak isotropy for Z. We apply this cross validation study to the precipitation data set for which we only keep the repetitions that contain no missing values (that is to say 92 repetitions). We have the following results

This means that in average the prediction at the monitoring sites is better in the D-space than in the G-space, so that we can claim that the model with deformation for the correlation of Z is better that the model without deformation. This has to be confirmed with the help of statistical tests to check if this improvement is significant or not.

5. Discussion

Simulated annealing appears to be a suitable tool for estimating a non-stationary structure. Combined with non-folding constraints, it gives the opportunity for the first time to estimate non-parametrically the bijective spatial deformation , in model (1), in such a way that the estimation remains bijective; however we wish to note two research questions

so far, the choice of the isotropic correlation is made by visual inspection, although less subjective approaches could be used [11]. An attempt to use a non-parametric family of correlation models has yet to be developed;
finally, one future direction will be to investigate statistical properties, such as consistency, of the non-parametric estimator of the deformation . A test of isotropy could be proposed too. It would consist of testing if $Phi(x_{i})=x_{i}$ for all (hypothesis of isotropy corresponding to the identical deformation in (1), provided that the network of the monitoring sites is dense enough in the G-space), against the alternative hypothesis that $Phi(x_{i}) neq x_{i}$ for at least one i (hypothesis of non-stationarity).

Acknowledgments

Olivier Perrin was supported by INRA, France; and by the European Union's research network "Statistical and Computational Methods for the Analysis of Spatial Data," Grant #ERB-FMRX-CT960095, while he was visiting the department of Mathematical Statistics at Chalmers University of Technology and Göteborg University in Sweden. The authors are grateful to Dominique Courault from Unité de Bioclimatologie, INRA-Avignon, France, for providing the precipitation data set, and to Jonathan Richard Shewchuk [21] for providing the program that performs the Delaunay triangulations. We also are grateful to Xavier Guyon for giving us the idea of this work.

References

Arts, E. and T.J. Kors, 1989. Simulated annealing and Boltzman machines: stochastic approaches to combinatorial optimization and neural computing. Wiley.

Azencott, R., Ed., 1992. Simulated annealing: parallelization techniques. Wiley.

Brown, P.J., N.D. L.E. J.V. Zidek, 1994. Multivariate spatial interpolation and exposure to air pollutants, The Canadian Journal of Statistics 22, pp. 489-505.

Cressie, N.A.C., 1993. Statistics for spatial data. Revised Edition: Wiley-Interscience, John Wiley and Sons, Inc. p. 900.

Geman, D., 1990. Random fields and inverse problem in imaging, L.N.M. No. 1427, Springer.

Geman, S. and D. Geman, 1984. Stochastic relaxation, Gibbs distribution, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Machine Intell. 6, pp. 721-741.

Guttorp, P. and P.D. Sampson, 1994. Methods for estimating heterogeneous spatial covariance functions with environmental applications, in: Patil, G.P. and Rao, C.R. (eds), Handbook of Statistics XII: Environmental Statistics, Elsevier/North Holland, New York, pp. 663-690.

Guttorp, P., P.D. Sampson, and K. Newman, 1992. Nonparametric estimation of non-stationary spatial covariance structure with application to monitoring network design, in: Walden, A. and Guttorp, P. Eds., Statistics in Environmental and Earth Sciences, Edward Arnold, London, pp. 39-51.

Host, G., H. Omre and P. Switzer, 1995. Spatial interpolation errors for monitoring data, Journal of the American Statistical Association 90, pp. 853-861.

Kirkpatrick, S., C.D. Gelatt, Jr. and M.P. Vecchi, 1983. Optimization by simulated annealing, Science 220, pp. 671-679.

Meiring, W., 1995. Estimation of heterogeneous space-time covariance, PhD thesis. University of Washington, Seattle, WA.

Meiring, W., P. Guttorp and P.D. Sampson, 1998.Computational issues in fitting spatial deformation models for heterogeneous spatial correlation, Computing Science and Statistics 29(1), (Scott, D.W., Ed.), pp. 409-417.

Meiring, W., P. Monestiez P.D. Sampson and P. Guttorp, 1997. Developments in the modelling of nonstationary spatial covariance structure from space-time monitoring data, in: Baafi, E.Y. and Schofield, N. (eds), Geostatistics Wollongong '96, Vol.1, Kluwer Academic Publishers, pp. 162-173.

Monestiez, P., P.D. Sampson and P. Guttorp, 1993. Modelling of heterogeneous spatial correlation structure by spatial deformation, Cahiers de Geostatistique, Fascicule 3, Compte Rendu des Journées de Géostatistique, 25-26 May 1993, Fontainebleau. Published by the École Nationale Supérieure des Mines de Paris.

Okabe, A., B. Boots and K. Sugihara, 1922. Spatial tessellations. Concepts and application of Voronoi diagrams. Wiley, Chichester.

Perrin, O. and W. Meiring, 1998. Identifiability for non-stationary spatial structure, Submitted for publication.

Perrin, O. and P. Monestiez, 1998. Modelling of non-stationary spatial structure using parametric radial basis deformations, to appear in: Soares, A., Gómez-Hernandez, J. and Froidevaux, R. (eds), geoENV98, Kluwer Academic Publishers.

Perrin, O. and R. Senoussi, 1998. Reducing non-stationary random fields to stationarity or isotropy using a space deformation, Submitted for publication.

Sampson, P. and P.D. Guttorp, 1992. Nonparametric estimation of nonstationary spatial covariance structure. JASA 87, pp. 108-119.

Sampson, P.D., P. Guttoro and W. Meiring, 1994. Spatio-temporal analysis of regional ozone data for operational evaluation of an air quality model, Proceedings of the Section on Statistics and the Environment, American Statistical Association.

Shewchuk, J. R., 1996. Triangle: engineering a 2-D quality mesh generator and Delaunay triangulator, First Workshop on Applied Computational Geometry (Philadelphia, Pennsylvania), pp. 124-133, ACM. Available online from http://www.cs.cmu.edu/ quake/triangle.research.html.